How to calculate the resistance of a wire - instructions with tables and formulas
Formula for calculating
Any calculations begin with a formula. The basic formula for calculating the resistance of a conductor is:
R = (ρ * l) / S
Where R is the resistance in Ohms, ρ is the resistivity, l is the length in m, S is the cross-sectional area of the wire in mm2.
This formula is suitable for calculating the resistance of a wire over its cross section and length. It follows from it that, depending on the length, the resistance changes, the longer - the more. And from the cross-sectional area - on the contrary, the thicker the wire (large cross-section), the lower the resistance. However, the value indicated by the letter ρ (Po) remains incomprehensible.
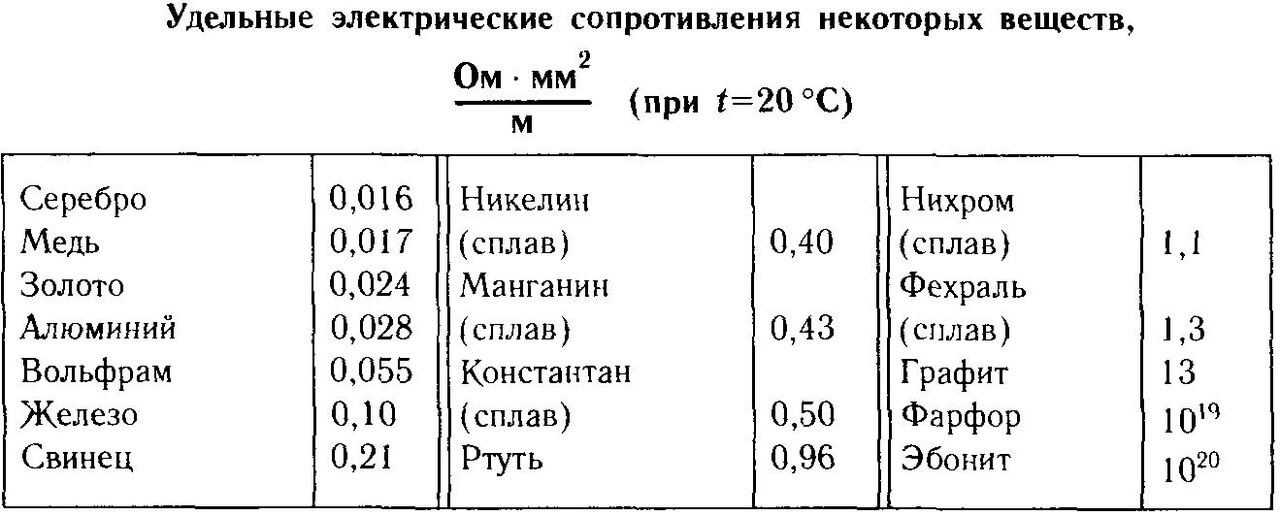
Resistivity
Resistivity is a tabular value, for each metal it has its own. It is needed for calculation and depends on the crystal lattice of the metal and the structure of atoms.
It can be seen from the table that silver has the smallest resistance; for a copper cable, it equals 0.017 Ohm * mm2/ m This dimension tells us how many Ohms are for a cross section of 1 millimeter square and a length of 1 meter.
By the way, silver plating is used in the contacts of switching devices, circuit breakers, relays, and more. It reduces contact resistanceincreases service life and reduces contact heating. Moreover, gold-plated contacts are used in the contacts of measuring and precision equipment due to the fact that they are weakly oxidized or not oxidized at all.
In aluminum, which was often used in electrical wiring before, the resistance is 1.8 times greater than that of copper, is 2.82 * 10-8 Ohm * mm2/ m The greater the resistance of the conductor, the more it is heated. Therefore, with the same cross-section, an aluminum cable can transfer less current than a copper one, this was the main reason why all modern electricians use copper wiring. In nichrome, which is used in heating devices, it is 100 times larger than in copper 1.1 * 10-6 Ohm * mm2/ m
Diameter calculation
In practice, it often happens that the cross-sectional area of a core is not known. Without this value, nothing can be calculated. To know it, you need to measure the diameter. If the core is thin, you can take a nail or any other rod, wind 10 turns of wire on it, measure the length of the resulting spiral with a regular ruler and divide by 10, so you know the diameter.
Well, or just measure with a caliper. Section calculation is performed according to the formula:
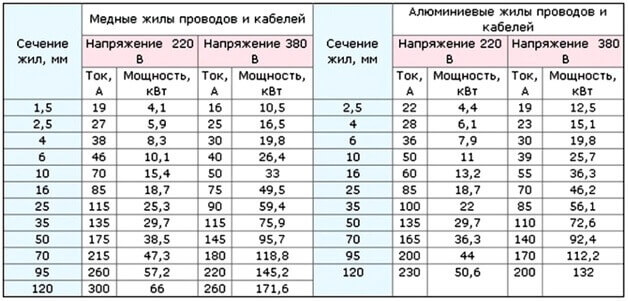
Are calculations required?
As we already said, the cross section of the wire is selected based on the estimated current and resistance of the metal from which the cores are made. The logic of choice is as follows: the cross section is selected in such a way that the resistance at a given length does not lead to significant voltage drops. In order not to carry out a number of calculations, for short lines (up to 10-20 meters) there are fairly accurate tables:
This table shows the typical values of the cross section of copper and aluminum conductors and the rated currents through them. For convenience, the load power that this line can withstand is indicated. Pay attention to the difference in currents and power at a voltage of 380V, of course, this is a three-phase power supply.
Finally, we recommend that you watch a video that details how to calculate the cross-section of the conductor, as well as examples of design work:
The calculation of the wire resistance comes down to using a pair of formulas, while you can download ready-made calculators from the Play Store for your smartphone, for example, “Electrodroid” or “Mobile Electrician”. This knowledge is useful for calculating heating devices, cable lines, fuses, and even today's popular electronic cigarette spirals.
Related materials:

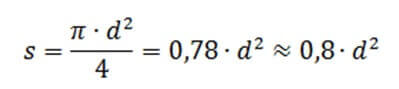





In the original formula, the cross-sectional area still seems to be in meters, otherwise the results do not agree with the tabular data (the resistance is too low).
Watch the video at the end of this article.