How to find the current strength in a circuit
If power and voltage are known
Suppose you need to find the current strength in a circuit, while you only know the voltage and power consumption. Then to determine it without resistance, use the formula:
P = UI
After simple, we get a formula for calculations
I = P / U
It should be noted that this expression is valid for DC circuits. But in calculations, for example, for an electric motor, its full power or cosine Phi is taken into account. Then for a three-phase motor it can be calculated as follows:
We find P taking into account the efficiency, usually it lies in the range of 0.75-0.88:
P1 = P2 / η
Here P2 is the active net power on the shaft, η - efficiency,both of these parameters usually indicate the nameplate.
We find the total power taking into account cosФ (it is also indicated on the nameplate):
S = P1 / cosφ
We determine the current consumption by the formula:
Inom = S / (1.73 · U)
Here 1.73 is the root of 3 (used for calculating a three-phase circuit), U is the voltage, depends on the engine turning on (a triangle or a star) and the number of volts in the network (220, 380, 660, etc.). Although in our country, 380V is most often found.
If voltage or power and resistance are known
But there are problems when you know the voltage on the circuit and the magnitude of the load, then to find the current without power use Ohm's law, with its help, we calculate the current strength through resistance and voltage.
I = U / R
But sometimes it happens that you need to determine the current strength without voltage, that is, when you only know the power of the circuit and its resistance. In this case:
P = UI
Moreover, according to Ohm’s same law:
U = IR
That:
P = i2* R
So we carry out the calculation according to the formula:
I2= P / R
Or take the expression on the right side of the expression under the root:
I = (P / R)1/2
If EMF, internal resistance and load are known
To student problems with a catch, there are cases when you are given the magnitude of the EMF and the internal resistance of the power source. In this case, you can determine the current strength in the circuit according to Ohm's law for a complete circuit:
I = E / (R + r)
Here E is the EMF, r is the internal resistance of the power source, and R is the load.
Joule-Lenz Law
Another task that even a more or less experienced student can enter into a stupor is to determine the strength of the current, if the time, resistance and the amount of heat released by the conductor are known.For this we recall Joule-Lenz law.
His formula looks like this:
Q = I2Rt
Then carry out the calculation as follows:
I2= QRt
Or add the right side of the equation under the root:
I = (Q / Rt)1/2
A few examples
As a conclusion, we propose to fix the information obtained on several examples of tasks in which you need to find the current strength.
1 task: Calculate I in a circuit of two resistors for serial connection and parallel connection. R resistors 1 and 2 Ohm, 12 volt power supply.
From the condition it is clear that you need to give two answers for each of the variants of the compounds. Then to find the current in series connection, first add up the resistance of the circuit to get the total.
R1+ R2= 1 + 2 = 3 Ohm
Then you can calculate the current strength according to Ohm's law:
I = U / R = 12/3 = 4 Amps
With a parallel connection of two elements, Rtotal can be calculated as follows:
Rtotal = (R1 * R2) / (R1 + R2) = 1 * 2/3 = 2/3 = 0.67
Then further calculations can be performed as follows:
I = 12 * 0.67 = 18A
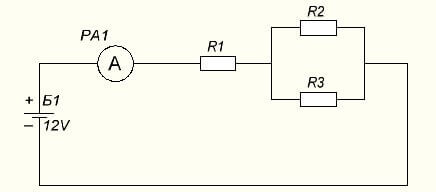
2 task: calculate the current for a mixed connection of elements. The output of the power supply is 24V, and the resistors are: R1 = 1 Ohm, R2 = 3 Ohm, R3 = 3 Ohm.
First of all, you need to find R total in parallel connected R2 and R3, according to the same formula that we used above.
Rpriv = (R2 * R3) / (R2 + R3) = (3 * 3) | (3 + 3) = 9/6 = 3/2 = 1.5 Ohm
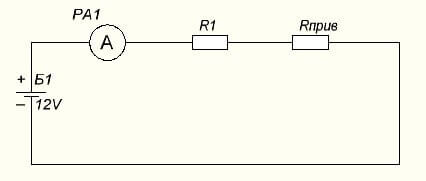
Now the circuit will take the form:
Next, we find the current according to the same Ohm's law:
I = U / (R1 + Rpriv) = 24 / (1 + 1.5) = 24 / 2.5 = 9.6 Amps
Now you know how to find the current strength, knowing the power, resistance and voltage. We hope that the provided formulas and calculation examples helped you learn the material!
Surely you do not know: