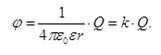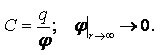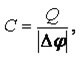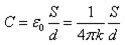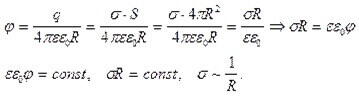How charges are distributed in a conductor when current flows
Charge carriers and their movement
A conductor is a substance in which carriers begin to move under the influence of the slightest external electric field. When there is no external field, the fields of positive ions and negative electrons cancel each other out. We examined a related issue in more detail and compared conductors, dielectrics and semiconductors in an article published earlier.
Consider a metal object that is in an electric field. The charge carriers begin to move under the influence of an external field due to the fact that the Coulomb forces begin to act on the charge carriers. Moreover, the direction of action of these forces on positive and negative carriers lies in a different direction. The movement stops if the sum of the intensities of the external and internal fields becomes zero, that is:
Erez = E internal + E external = 0
In this case, the field strength is equal to:
E = dF / dt
If the tension is zero, then the potential inside the body is equal to some constant number. This will become clear if we express the potential from this formula and integrate, that is:
Positive ions and electrons from the entire body volume rush to its surface in order to compensate for the tension electric field. Then, inside the conductor, the electric field becomes equal to zero, since it is balanced by charge carriers from its surface.
Interesting! A surface on which the same potential is present at all points is called equipotential.
If we consider this issue in more detail, then when a conductor is introduced into an electric field, positive ions move against its lines of force, and negative electrons in the same direction. This happens until they are distributed, and the field in the conductor becomes equal to zero. Such charges are called induced or excess.
Important! When the charges are communicated to the conductive material, they are distributed so that an equilibrium state is reached. The same charges will repel and tends in accordance with the direction of the lines of force of the electric field.
It follows that the work of moving charge carriers is zero, which is equal to the potential difference. Then the potential in different sections of the conductor is equal to a constant number and does not change.It is important to know that in a dielectric, in order to tear off a charge carrier, for example, an electron from an atom, great forces must be applied. Therefore, the described phenomena in a general sense are observed on conductive bodies.
Electric capacity of a solitary conductor
First, consider the concept of a solitary conductor. This is a conductor that is remote from other charged conductors and bodies. Moreover, the potential on it will depend on its charge.
The electrical capacity of a solitary conductor is the ability of a conductor to hold a distributed charge. First of all, it depends on the shape of the conductor.
If two such bodies are separated by a dielectric, for example, air, mica, paper, ceramics, etc. - get a capacitor. Its capacity depends on the distance between the plates and their area, as well as on the potential difference between them.
The formulas describe the dependence of capacitance on the potential difference and on the geometric dimensions of a flat capacitor. Learn more about what is electric capacity, you can from our separate article.
Charge distribution and body shape
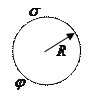
So, the distribution density of charge carriers depends on the shape of the conductor. Consider this with the example of formulas for a sphere.
Suppose that we have a certain metallic charged sphere, with radius R, charge density on the surface G and potential F. Then:
From the last derived formula, we can understand that the density is approximately inversely proportional to the radius of the sphere.
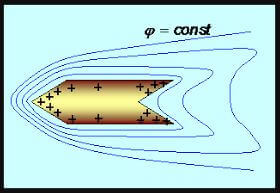
That is, the more convex and sharp the object, the greater the density of carriers in this place. On concave surfaces, the density is minimal. This can be seen in the video:
Practical application
If you take into account the above, it is worth noting that the current flows through the cable and is distributed, as if by the outer diameter of the pipe. This is due to the characteristics of the distribution of electrons in a conducting body.
It is curious that when current flows in systems with a high-frequency current, a skin effect is observed. This is the distribution of charges on the surface of the conductors. But in this case, an even thinner “conducting” layer is observed.
What does it mean? This suggests that for the flow of current of a similar magnitude with a network frequency of 50 Hz and a frequency of 50 kHz in a high-frequency circuit, a larger cross section of the conductive core will be required. In practice, this is observed in switching power supplies. It is precisely such currents that flow in their transformers. To increase the cross-sectional area, either choose a thick wire, or winding the windings with several veins at once.
The dependence of the density distribution on the surface shape described in the previous section is used in practice in lightning protection systems. It is known that to protect against lightning damage, one of the types of lightning protection, for example a lightning rod, is installed. On its surface, charged particles accumulate, due to which the discharge occurs precisely in it, which again confirms what was said about their distribution.
Finally, we recommend watching a video in which, in simple words, it explains and clearly shows how the charges are distributed in the conductor:
This is all we wanted to tell you about how the charge distribution in the conductor occurs when current flows. We hope that the information provided was understandable and useful for you!
Related materials: