กฎหมายที่หนึ่งและสองของ Kirchhoff - คำอธิบายที่ไม่แพง
กฎข้อแรกของ Kirchhoff
คำจำกัดความของกฎหมายฉบับแรกคือ:“ผลรวมพีชคณิตของกระแสที่ไหลผ่านโหนดเป็นศูนย์” คุณสามารถพูดรูปแบบที่ต่างออกไปเล็กน้อย: "มีกี่กระแสที่ไหลเข้าสู่โหนดจำนวนเดียวกันไหลออกซึ่งบ่งบอกถึงความมั่นคงของกระแส”.
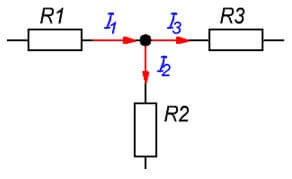
โหนดของลูกโซ่คือจุดเชื่อมต่อของสาขาสามสาขาขึ้นไป กระแสในกรณีนี้มีการกระจายตามสัดส่วนกับความต้านทานของแต่ละสาขา
ผม1= ฉัน2+ ฉัน3
รูปแบบการบันทึกนี้ใช้ได้กับวงจร DC หากคุณใช้กฎหมาย Kirchhoff แรกสำหรับวงจรกระแสสลับจะมีการใช้ค่าแรงดันไฟฟ้าทันทีโดยใช้ตัวอักษรİและเขียนในรูปแบบที่ซับซ้อนและวิธีการคำนวณยังคงเหมือนเดิม:
แบบฟอร์มที่ซับซ้อนจะต้องคำนึงถึงทั้งองค์ประกอบที่ใช้งานและปฏิกิริยา
กฎข้อที่สองของ Kirchhoff
หากครั้งแรกที่อธิบายถึงการกระจายของกระแสในสาขากฎหมาย Kirchhoff ที่สองคือ:“ผลรวมของแรงดันไฟฟ้าตกในวงจรเท่ากับผลรวมของ EMF ทั้งหมด”กล่าวอย่างง่าย ๆ ถ้อยคำอ่านดังนี้:“ EMF ที่ใช้กับส่วนของวงจรจะถูกกระจายในองค์ประกอบของวงจรนี้ตามสัดส่วนของความต้านทานคือ ตามกฎหมายของโอห์ม "
ในขณะที่กระแสสลับมันฟังดูเหมือนว่า:“ผลรวมของแอมพลิจูดของ EMF ที่ซับซ้อนเท่ากับผลรวมของแรงดันไฟฟ้าเชิงซ้อนที่ลดลงในองค์ประกอบ ".
Z คืออิมพีแดนซ์หรือความต้านทานเชิงซ้อนรวมทั้งส่วนต้านทานและส่วนรีแอกทีฟ (ตัวเหนี่ยวนำและความจุ) ซึ่งขึ้นอยู่กับความถี่ของกระแสไฟฟ้าสลับ ด้านล่างเป็นสูตรของความต้านทานเชิงซ้อนของตัวเก็บประจุและตัวเหนี่ยวนำ:
นี่คือภาพที่แสดงด้านบน:
แล้ว:
วิธีการคำนวณสำหรับกฎหมายที่หนึ่งและสองของ Kirchhoff
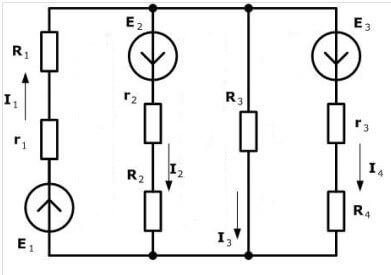
ลองนำเนื้อหาทางทฤษฎีมาปฏิบัติ เพื่อให้สัญญาณถูกต้องในสมการคุณต้องเลือกทิศทางของวงจร ลองดูที่แผนภาพ:
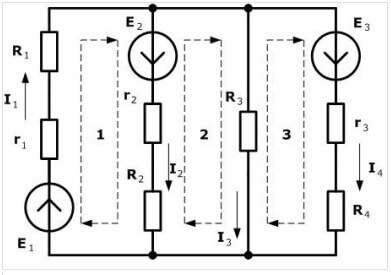
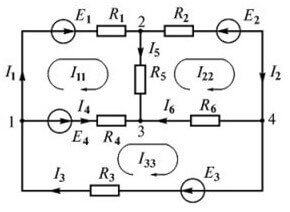
เราแนะนำให้เลือกทิศทางตามเข็มนาฬิกาและทำเครื่องหมายไว้ในภาพ:
เส้นประประแสดงวิธีการตามเส้นทางเมื่อทำการสมการ
ขั้นตอนต่อไปคือการเขียนสมการตามกฎหมายของ Kirchhoff ครั้งแรกที่เราใช้ครั้งที่สองเราใส่เครื่องหมายด้วยวิธีนี้: เครื่องหมายลบจะถูกวางไว้หน้าแรงเคลื่อนไฟฟ้าถ้ามันหมุนทวนเข็มนาฬิกา (ทิศทางที่เราเลือกในขั้นตอนก่อนหน้า) จากนั้นสำหรับแรงเคลื่อนไฟฟ้าตามเข็มนาฬิกาที่เราใส่เครื่องหมายลบ เราเขียนสำหรับแต่ละวงจรโดยคำนึงถึงสัญญาณ
สำหรับครั้งแรกที่เราดูทิศทางของ EMF มันสอดคล้องกับเส้นประประตั้ง E1 บวก E2:
สำหรับวินาที:
สำหรับที่สาม:
สัญญาณสำหรับ IR (แรงดันไฟฟ้า) ขึ้นอยู่กับทิศทางของกระแสลูป ที่นี่กฎการลงชื่อจะเหมือนกับในกรณีก่อนหน้า
IR ถูกเขียนด้วยเครื่องหมายบวกถ้ากระแสไหลในทิศทางของวงจรบายพาสทิศทาง และมีเครื่องหมาย“ -” หากกระแสไหลตรงกับทิศทางของวงจร
ทิศทางของการเคลื่อนที่ผ่านวงจรเป็นปริมาณที่มีเงื่อนไข มันเป็นสิ่งจำเป็นสำหรับการจัดเรียงของสัญญาณในสมการเท่านั้นมันถูกเลือกโดยพลการและไม่มีผลต่อความถูกต้องของการคำนวณ ในบางกรณีทิศทางบายพาสที่เลือกไม่ดีอาจทำให้การคำนวณซับซ้อนขึ้น แต่สิ่งนี้ไม่สำคัญ
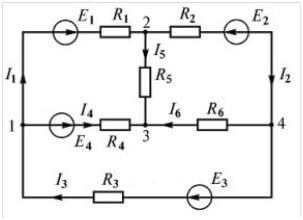
พิจารณาวงจรอื่น:
มีแหล่งข้อมูล EMF มากถึงสี่แห่ง แต่ขั้นตอนการคำนวณเหมือนกันก่อนอื่นเราเลือกทิศทางสำหรับการสร้างสมการ
ตอนนี้คุณต้องสร้างสมการตามกฎข้อแรกของ Kirchhoff สำหรับโหนดแรก (รูปที่ 1 ด้านซ้ายของไดอะแกรม):
ผม3 ไหลเข้าและฉัน1, ผม4 มันดังนี้ดังนั้นสัญญาณ สำหรับวินาที:
สำหรับที่สาม:
คำถาม: "มีสี่โหนดและมีเพียงสามสมการทำไม”ความจริงก็คือจำนวนของสมการของกฎ Kirchhoff แรกเท่ากับ:
ยังไม่มีข้อความสมการ= nนอต-1
เหล่านั้น มีเพียง 1 สมการที่น้อยกว่าโหนดเนื่องจาก นี่เพียงพอที่จะอธิบายกระแสในกิ่งไม้ทั้งหมดฉันแนะนำอีกครั้งเพื่อขึ้นไปยังวงจรและตรวจสอบว่ากระแสทั้งหมดถูกเขียนในสมการหรือไม่
ตอนนี้เราดำเนินการสร้างสมการตามกฎข้อที่สอง สำหรับวงจรหลัก:
สำหรับวงจรที่สอง:
สำหรับวงจรที่สาม:
หากเราแทนที่ค่าของแรงดันไฟฟ้าและความต้านทานที่แท้จริงแสดงว่ากฎข้อที่หนึ่งและที่สองนั้นยุติธรรมและเป็นจริง นี่เป็นตัวอย่างง่าย ๆ ในทางปฏิบัติแล้วปัญหามากมายที่ต้องแก้ไข
ข้อสรุป. สิ่งสำคัญเมื่อคำนวณด้วยความช่วยเหลือของกฎหมาย Kirchhoff ที่หนึ่งและที่สองคือการปฏิบัติตามกฎสำหรับการสร้างสมการคือ คำนึงถึงทิศทางของการไหลของกระแสและบายพาสวงจรเพื่อการจัดสัญญาณที่ถูกต้องสำหรับแต่ละองค์ประกอบของวงจร
กฎของ Kirchhoff สำหรับวงจรแม่เหล็ก
การคำนวณวงจรแม่เหล็กก็มีความสำคัญในด้านวิศวกรรมไฟฟ้าเช่นกันทั้งสองกฎหมายพบการใช้งานที่นี่ สาระสำคัญยังคงเหมือนเดิม แต่การเปลี่ยนแปลงประเภทและขนาดลองดูที่รายละเอียดเพิ่มเติม ก่อนอื่นคุณต้องจัดการกับแนวคิด
Magnetomotive force (MDS) ถูกกำหนดโดยผลคูณของจำนวนรอบของขดลวดโดยกระแสผ่าน:
F = w * i
แรงดันสนามแม่เหล็กเป็นผลคูณของความเข้มของสนามแม่เหล็กและกระแสผ่านส่วนวัดเป็นแอมแปร์:
ยูม.= H * I
หรือฟลักซ์แม่เหล็กผ่านความต้านทานแม่เหล็ก:
ยูม.= F * Rม.
L คือความยาวเฉลี่ยของพล็อตคือμR และμ0 - การซึมผ่านของแม่เหล็กสัมพัทธ์และสัมบูรณ์
เราเขียนกฎ Kirchhoff แรกสำหรับวงจรแม่เหล็กโดยการเปรียบเทียบ
นั่นคือผลรวมของฟลักซ์แม่เหล็กทั้งหมดผ่านโหนดเป็นศูนย์ คุณสังเกตเห็นว่าเสียงเกือบเหมือนวงจรไฟฟ้าหรือไม่?
จากนั้นกฎข้อที่สองของ Kirchhoff ดูเหมือนว่า“ ผลรวมของ MDS ในวงจรแม่เหล็กเท่ากับผลรวมของ UM ความเครียดของแม่เหล็ก
ฟลักซ์แม่เหล็กมีค่าเท่ากับ:
สำหรับสนามแม่เหล็กสลับ:
มันขึ้นอยู่กับแรงดันไฟฟ้าที่คดเคี้ยวเท่านั้นและไม่ขึ้นกับพารามิเตอร์ของวงจรแม่เหล็ก
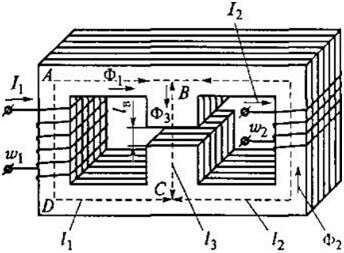
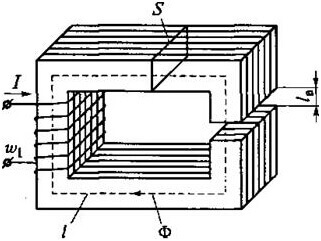
ลองพิจารณาตัวอย่างนี้:
จากนั้นสำหรับ ABCD เราจะได้รับสูตรต่อไปนี้:
สำหรับวงจรที่มีช่องว่างอากาศความสัมพันธ์ต่อไปนี้เป็นจริง:
ความต้านทานแม่เหล็ก:
และความต้านทานของช่องว่างอากาศ (ด้านขวาบนแกน):
โดยที่ S คือพื้นที่ของแกนกลาง
เพื่อทำความเข้าใจเนื้อหาและตรวจสอบความแตกต่างของการใช้กฎอย่างเห็นได้ชัดเราขอแนะนำให้คุณทำความคุ้นเคยกับการบรรยายที่ให้ไว้ในวิดีโอ:
การค้นพบของกุสตาฟ Kirchhoff ทำให้มีส่วนสำคัญต่อการพัฒนาวิทยาศาสตร์โดยเฉพาะอย่างยิ่งวิศวกรรมไฟฟ้าด้วยความช่วยเหลือของพวกเขามันค่อนข้างง่ายในการคำนวณวงจรไฟฟ้าหรือแม่เหล็กกระแสในมันและแรงดันไฟฟ้า เราหวังว่ากฎของ Kirchhoff สำหรับวงจรไฟฟ้าและสนามแม่เหล็กจะชัดเจนสำหรับคุณมากขึ้น
วัสดุที่คล้ายกัน:

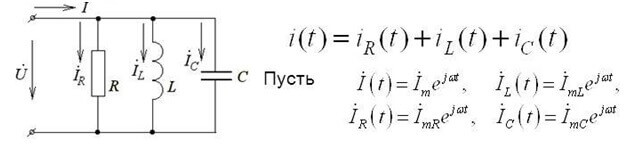
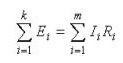
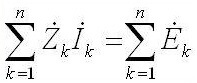
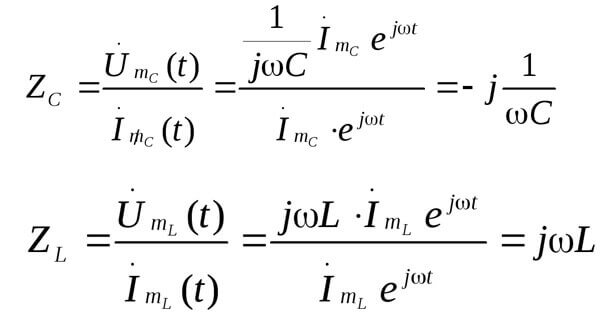

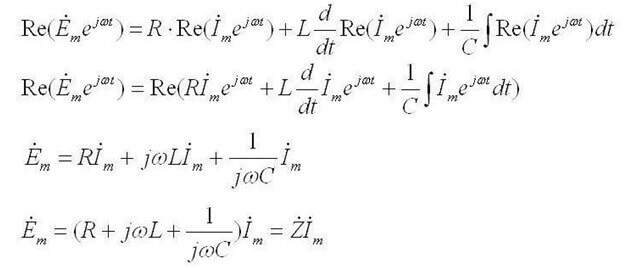
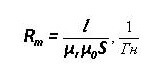
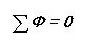
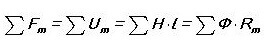
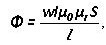
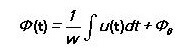
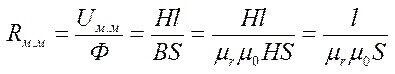
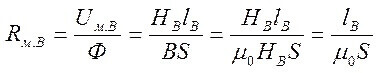


เมื่อเราเขียนกฎตามกฎหมายของ Kirchhoff นั่นก็คือคำอธิบายที่ดีสำหรับคุณข้อแรก ทำไมไม่มีคำอธิบายสำหรับที่สองและสามเมื่อทุกอย่างไม่ชัดเจนมากขึ้น? I2 ไหลเข้ามาอย่างชัดเจน แต่ด้วยเหตุผลบางอย่างเขามีสัญญาณเชิงบวก
ในสมการที่สามดังนั้นโดยทั่วไปแล้วทั้งสามฉันไหลเข้า ทำไมพวกเขาถึงเป็นบวก?
โปรดทราบว่าในตอนต้นของบทความสมการนั้นจะถูกพิจารณาในรูปแบบ I1 = I2 + I3 หากคุณถ่ายโอนทุกอย่างไปทางด้านซ้ายของสมการ I1-I2-I3 = 0 สิ่งเดียวกันก็ทำที่นั่น
สำหรับโหนดที่สอง:
I1 = I5 + I2
การเคลื่อนไหวทุกอย่างในทิศทางเดียวจะออกมา:
I1-I5-I2 = 0
เมื่อเปรียบเทียบกับทิศทางของวงจรบายพาสมันจะกลายเป็นที่ชัดเจนว่ามันเป็นการดีกว่าที่จะเปลี่ยนสัญญาณนั่นคือคูณด้วยลบ 1
จะออกมา
-I1 + I5 + I2 = 0
ซึ่งเทียบเท่า
I2 + I5-I1 = 0