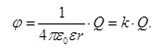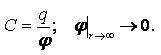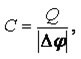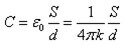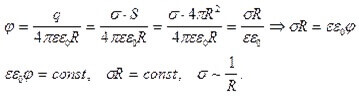Hur laddningar fördelas i en ledare när strömmen flyter
Laddningsföretag och deras rörelse
En ledare är ett ämne där bärare börjar röra sig under påverkan av det minsta externa elektriska fältet. När det inte finns något yttre fält avbryter fälten för positiva joner och negativa elektroner varandra. Vi undersökte en relaterad fråga mer detaljerat och jämfördes ledare, dielektrik och halvledare i en artikel publicerad tidigare.
Tänk på ett metallföremål som finns i ett elektriskt fält. Laddningsbärarna börjar röra sig under påverkan av ett yttre fält på grund av att Coulomb-styrkorna börjar agera på laddningsbärarna. Dessutom ligger dessa krafts handlingsriktning på positiva och negativa bärare i en annan riktning. Rörelsen stannar om summan av intensiteten för de yttre och interna fälten blir noll, det vill säga:
Erez = E intern + E extern = 0
I detta fall är fältstyrkan lika med:
E = dF / dt
Om spänningen är noll, är potentialen i kroppen lika med ett konstant antal. Detta kommer att bli tydligt om vi uttrycker potentialen från denna formel och integrerar, det vill säga:
Positiva joner och elektroner från hela kroppens volym rusar till ytan för att kompensera för spänningen elektriskt fält. Därefter, inuti ledaren, blir det elektriska fältet lika med noll, eftersom det balanseras av laddningsbärare från dess yta.
Intressant! En yta på vilken samma potential finns på alla punkter kallas ekvipotential.
Om vi överväger detta problem mer detaljerat, när en ledare införs i ett elektriskt fält, rör sig positiva joner mot dess kraftlinjer och negativa elektroner i samma riktning. Detta händer tills de är fördelade och fältet i ledaren blir lika med noll. Sådana avgifter kallas inducerade eller överskott.
Viktigt! När laddningarna kommuniceras till det ledande materialet fördelas de så att ett jämviktstillstånd uppnås. Samma laddningar kommer att avvisas och tenderar i enlighet med riktningen för kraftlinjerna för det elektriska fältet.
Av detta följer att arbetet med att flytta laddningsbärare är noll, vilket är lika med potentialskillnaden. Då är potentialen i olika sektioner av ledaren lika med ett konstant antal och förändras inte.Det är viktigt att veta att i ett dielektrikum, för att riva av en laddningsbärare, till exempel en elektron från en atom, måste stora krafter appliceras. Därför observeras de beskrivna fenomenen i allmän mening på ledande organ.
Elektrisk kapacitet för en ensamledare
Först bör du tänka på begreppet en ensamledare. Detta är en ledare som är avlägsen från andra laddade ledare och kroppar. Dessutom kommer potentialen för det att bero på dess laddning.
En elektrisk ledares elektriska kapacitet är en ledares förmåga att hålla en distribuerad laddning. Först och främst beror det på ledarens form.
Om två sådana kroppar separeras med en dielektrik, till exempel luft, glimmer, papper, keramik, etc. - få en kondensator. Dess kapacitet beror på avståndet mellan plattorna och deras område, liksom av potentialskillnaden mellan dem.
Formlerna beskriver kapacitansberoendet av potentialskillnaden och de platta kondensatorns geometriska dimensioner. Läs mer om vad är elektrisk kapacitet, kan du från vår separata artikel.
Laddningsfördelning och kroppsform
Således beror fördelningstätheten för laddningsbärare på ledarens form. Tänk på detta med exemplet med formler för en sfär.
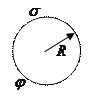
Anta att vi har en viss metallladdad sfär, med radie R, laddningstäthet på ytan G och potential F. Sedan:
Från den sista härledda formeln kan vi förstå att densiteten är ungefär omvänt proportionell mot sfärens radie.
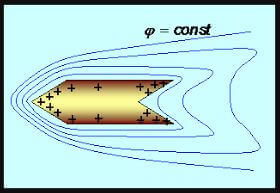
Det vill säga, ju mer konvext och skarpt objektet är, desto större är tätheten hos bärare på denna plats. På konkava ytor är densiteten minimal. Detta kan ses i videon:
Praktisk tillämpning
Om du tar hänsyn till ovanstående är det värt att notera att strömmen flyter genom kabeln och distribueras, som om rörets ytterdiameter är. Detta beror på egenskaperna hos distributionen av elektroner i en ledande kropp.
Det är konstigt att när ström flyter i system med högfrekvensström, observeras en hudeffekt. Detta är fördelningen av laddningar på ledarnas yta. Men i detta fall observeras ett ännu tunnare "ledande" skikt.
Vad betyder detta? Detta antyder att för strömflödet av liknande storlek med en nätfrekvens på 50 Hz och en frekvens på 50 kHz i en högfrekvenskrets krävs ett större tvärsnitt av den ledande kärnan. I praktiken observeras detta vid växling av strömförsörjning. Det är just sådana strömmar som flyter i deras transformatorer. För att öka tvärsnittsområdet väljer du antingen en tjock tråd eller lindar lindningarna med flera vener samtidigt.
Beroendet av densitetsfördelningen på ytformen som beskrivs i föregående sektion används i praktiken i blixtskyddssystem. Det är känt att en av de typer av blixtskydd, till exempel en blixtstång, installeras för att skydda mot blixtnedslag. På ytan ackumuleras laddade partiklar, på grund av vilken urladdningen sker exakt i den, vilket igen bekräftar vad som sades om deras distribution.
Slutligen rekommenderar vi att du tittar på en video där det med enkla ord förklaras och grafiskt visas hur laddningarna fördelas i ledaren:
Detta är allt vi ville berätta om hur laddningsfördelningen i ledaren sker när strömmen flyter. Vi hoppas att den information som lämnades var förståelig och användbar för dig!
Relaterade material: