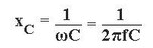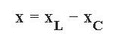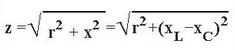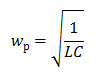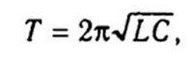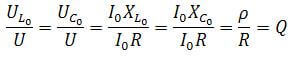Vad är resonansen för strömmar och spänningar
Induktansreaktans och kapacitans
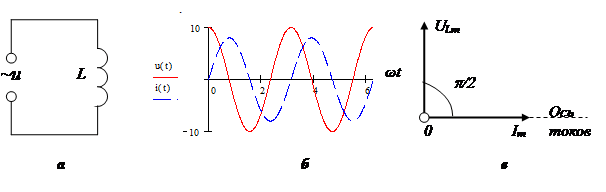
Induktans är kroppens förmåga att ackumulera energi i ett magnetfält. Det kännetecknas av en fördröjning av ström från spänning i fas. Typiska induktiva element är choker, spolar, transformatorer, elmotorer.
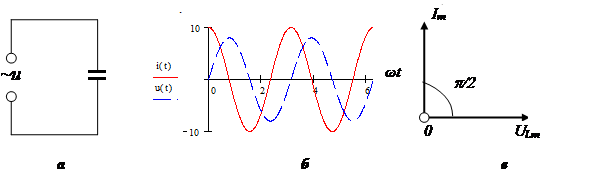
Kapacitet avser element som lagrar energi genom ett elektriskt fält. Kapacitiva element kännetecknas av en fasfördröjning av spänningen från strömmen. Kapacitiva element: kondensatorer, varicaps.
Deras grundläggande egenskaper anges, nyanserna i denna artikel beaktas inte.
Förutom de listade elementen har andra också en viss induktans och kapacitet, till exempel i elektriska kablar fördelade längs dess längd.
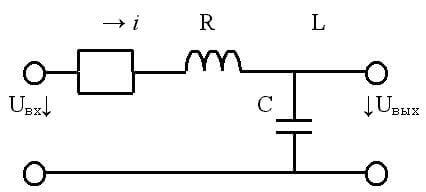
Kapacitans och induktans i en växelströmskrets
Om i DC-kretsar är kapacitansen i allmän mening en trasig del av kretsen, och induktansen är en ledare, är i växelvisa kondensatorer och spolar en reaktiv analog av ett motstånd.
Induktorns reaktans bestäms av formeln:
Vektor diagram:
Kondensatorreaktans:
Här är vinkelfrekvensen, f är frekvensen i sinusformad strömkrets, L är induktansen, C är kapacitansen.
Vektor diagram:
Det är värt att notera att vid beräkningen av reaktiva element anslutna i serie används formeln:
Observera att den kapacitiva komponenten tas med ett minustecken. Om den aktiva komponenten (motståndet) också finns i kretsen, lägg sedan till enligt formeln för Pythagoras teorem (baserat på vektordiagrammet):
Vad beror reaktans på? Reaktiva egenskaper beror på kapacitansen eller induktansen, liksom på växelströmens frekvens.
Om du tittar på formeln för den reaktiva komponenten, kan du se att för vissa värden på den kapacitiva eller induktiva komponenten, deras skillnad kommer att vara noll, kommer bara motståndet kvar i kretsen. Men detta är inte alla funktionerna i en sådan situation.
Spänningsresonans
Om en kondensator och en induktor är seriekopplade med en generator, kommer, förutsatt att deras reaktans är lika, att uppstå en spänningsresonans. I detta fall bör den aktiva delen Z vara så liten som möjligt.
Det är värt att notera att induktans och kapacitans endast har reaktiva egenskaper endast i idealiserade exempel. I verkliga kretsar och element är ledarnas aktiva motstånd alltid närvarande, även om det är extremt litet.
Vid resonans inträffar ett energiutbyte mellan induktorn och kondensatorn. I idealiska exempel, under den initiala anslutningen av en energikälla (generator), ackumuleras energi i kondensatorn (eller induktorn) och efter att den har stängts av inträffar ostämda svängningar på grund av detta utbyte.
Spänningarna vid induktorerna och kapacitanserna är ungefär desamma enligt Ohms lag:
U = I / X
Där X är Xc-kapacitiv respektive XL-induktans.
En krets bestående av induktans och kapacitans kallas en oscillerande krets. Dess frekvens beräknas med formeln:
Svängningsperioden bestäms av Thompson-formeln:
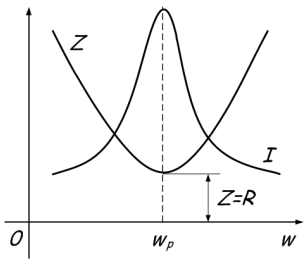
Eftersom reaktansen beror på frekvensen ökar induktansmotståndet med ökande frekvens och minskar vid kapacitansen. När motstånden är lika, reduceras det totala motståndet kraftigt, vilket återspeglas i diagrammet:
Kretsens huvudegenskaper är kvalitetsfaktorn (Q) och frekvensen. Om vi betraktar kretsen som en fyra-terminal reduceras dess överföringskoefficient efter enkla beräkningar till kvalitetsfaktorn:
K = q
Och spänningen vid kretsens terminaler ökar i proportion till kretsens överföringskoefficient (kvalitetsfaktor).
UK = Uin * Q
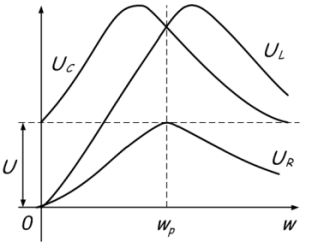
Med spänningsresonans, ju högre kvalitetsfaktor, desto större kommer spänningen på kretselementen att överskrida den anslutna generatorens spänning. Spänningen kan öka tiotals eller hundratals gånger. Detta visas i grafen:
Kraftförluster i kretsen beror bara på närvaron av aktivt motstånd. Energi från kraftkällan tas bara för att upprätthålla fluktuationer.
Kraftfaktorn kommer att vara lika med:
cosФ = 1
Denna formel visar att förluster uppstår på grund av aktiv effekt:
S = P / Cosph
Resonansströmmar
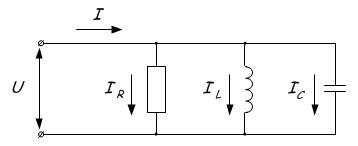
Strömresonans observeras i kretsar där induktansen och kapacitansen är parallellt anslutna.
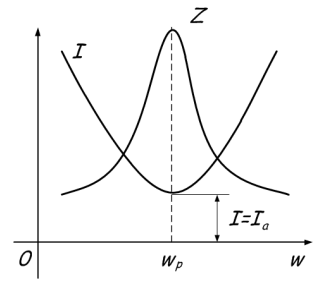
Fenomenet består i flödet av stora strömmar mellan kondensatorn och spolen, vid nollström i kretsens ogrenade del. Detta beror på att när resonansfrekvensen uppnås ökar den totala resistansen Z. Eller helt enkelt låter det så här - vid resonanspunkten uppnås det maximala totalvärdet på motståndet Z, varefter ett av motstånden ökar och det andra minskar, beroende på om frekvensen ökar eller minskar. Detta visas grafiskt:
I allmänhet liknar allt det föregående fenomenet, villkoren för uppkomsten av aktuell resonans är följande:
- Effektfrekvensen liknar resonanten vid kretsen.
- Konduktiviteterna för induktansen och kapacitansen för växelström är lika med BL = Bc, B = 1 / X.
Praktisk applikation
Tänk på fördelarna och skadorna av resonansströmmar och spänningar. Den största fördelen med fenomenet resonans medförs i radiosändningsutrustning. I enkla ord har mottagarkretsen en spole och en kondensator ansluten till antennen. Genom att ändra induktansen (till exempel flytta kärnan) eller värdet på kapacitansen (till exempel en luftvariabel kondensator) justerar du resonansfrekvensen. Som ett resultat stiger spänningen på spolen och mottagaren fångar en viss radiovåg.
Dessa fenomen kan vara skadliga inom elektroteknik, till exempel på kabellinjer. En kabel är en induktans och kapacitans fördelad längs längden om spänning matas till en lång linje i viloläge (när lasten inte är ansluten till kabelns ände motsatt kraftkällan). Därför finns det en risk att en isolering går sönder, för att undvika detta är en lastförkoppling ansluten.En liknande situation kan också leda till att elektroniska komponenter, mätinstrument och annan elektrisk utrustning misslyckas - detta är farliga konsekvenser av detta fenomen.
Slutsats
Resonansen för spänningar och strömmar är ett intressant fenomen att vara medveten om. Det observeras endast i induktiv-kapacitiva kretsar. I kretsar med stora aktiva motstånd kan det inte uppstå. För att sammanfatta, svara kort på de viktigaste frågorna om detta ämne:
- Var och i vilka kedjor observeras resonansfenomenet?
I induktiva kapacitiva kretsar.
- Vilka är villkoren för resonans av strömmar och spänningar?
Det inträffar under förutsättning av lika reaktans. Kretsen måste ha ett minimum aktivt motstånd, och strömförsörjningens frekvens sammanfaller med kretsens resonansfrekvens.
- Hur hittar jag resonansfrekvensen?
I båda fallen med formeln:w = (1 / LC) ^ (1/2)
- Hur kan man eliminera fenomenet?
Genom att öka motståndet i kretsen eller ändra frekvensen.
Nu vet du vad resonansen för strömmar och spänningar är, vilka är villkoren för dess förekomst och praktiska tillämpningar. För att konsolidera materialet rekommenderar vi att du tittar på en användbar video om ämnet:
Relaterade material: