Hukum arus penuh dengan kata mudah
Subjek yang dikenal oleh banyak orang, berjudul "Kejuruteraan Elektrik", memuat dalam programnya serangkaian undang-undang asas yang menentukan prinsip interaksi fizikal untuk medan magnet. Mereka memperluas kesannya kepada pelbagai elemen peranti elektrik, serta struktur dan persekitarannya. Fizik proses yang berlaku di dalamnya berkaitan dengan konsep asas seperti arus elektrik dan medan. Hukum arus total menetapkan hubungan antara pergerakan cas elektrik dan medan magnet yang diciptakan olehnya (lebih tepatnya, intensiti). Sains moden mendakwa bahawa aplikasinya merangkumi hampir semua persekitaran.
Intipati undang-undang
Undang-undang yang dipertimbangkan, yang berlaku dalam rangkaian magnetik, menentukan hubungan kuantitatif berikut antara komponen penyusunnya. Peredaran vektor medan magnet dalam gelung tertutup berkadar dengan jumlah arus yang menembusnya. Untuk memahami makna fizikal undang-undang arus penuh, anda perlu membiasakan diri dengan gambaran grafik mengenai proses yang dijelaskan olehnya.
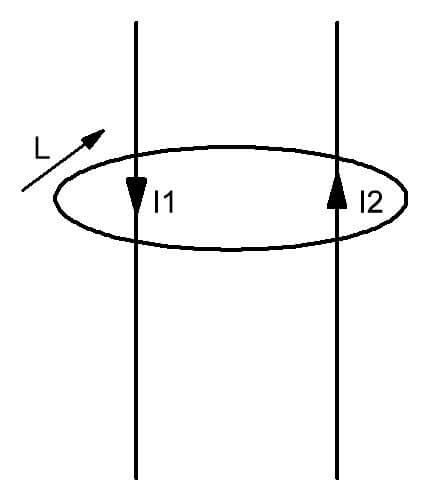
Ini dapat dilihat dari gambar bahawa kira-kira dua konduktor dengan arus I1 dan I2 mengalir melaluinya, sebuah medan terbentuk, dibatasi oleh litar L. Ia diperkenalkan sebagai angka tertutup yang dibayangkan secara mental, bidangnya ditembusi oleh konduktor dengan cas bergerak. Dengan kata mudah, undang-undang ini dapat dinyatakan sebagai berikut. Di hadapan beberapa aliran elektrik melalui permukaan khayalan khayalan yang diliputi oleh litar L, medan magnet dengan pengedaran tegangan tertentu terbentuk di dalamnya.
Untuk arah positif vektor sesuai dengan hukum untuk kontur litar magnet dipilih mengikut arah jam. Ia juga dapat dibayangkan.
Definisi bidang eddy seperti yang dibuat oleh arus menunjukkan bahawa arah setiap arus boleh sewenang-wenangnya.
Untuk rujukan! Struktur medan yang diperkenalkan dan alat yang menggambarkannya harus dibezakan dari peredaran vektor elektrostatik "E", yang selalu sama dengan sifar melewati litar. Hasilnya, bidang seperti ini merujuk kepada struktur yang berpotensi. Peredaran vektor "B" medan magnet tidak pernah sifar. Itulah sebabnya ia disebut "pusaran".
Konsep asas
Sesuai dengan undang-undang yang dipertimbangkan, pendekatan sederhana berikut digunakan untuk mengira medan magnet. Jumlah arus ditunjukkan sebagai jumlah beberapa komponen yang mengalir melalui permukaan yang diliputi oleh litar tertutup L. Pengiraan teoritis dapat ditunjukkan sebagai berikut:
- Jumlah arus elektrik yang mengalir melalui litar Σ I adalah jumlah vektor I1 dan I2.
- Dalam contoh ini, untuk menentukannya, gunakan formula:
ΣI = I1 - I2 (tolak sebelum penggal kedua bermaksud bahawa arah arus bertentangan). - Mereka, pada gilirannya, ditentukan berdasarkan undang-undang yang dikenal dalam kejuruteraan elektrik (peraturan) gimlet.
Medan magnet sepanjang kontur dikira berdasarkan pengiraan yang diperoleh dengan teknik khas. Untuk mencarinya, perlu mengintegrasikan parameter ini di atas L menggunakan persamaan Maxwell yang disajikan dalam salah satu bentuk.Ia boleh digunakan dalam bentuk pembezaan, tetapi ini sedikit sebanyak akan menyukarkan pengiraannya.
Pendekatan Bersepadu Ringkas
Sekiranya kita menggunakan perwakilan pembezaan, menyatakan hukum terkini dalam bentuk yang disederhanakan akan sangat sukar (dalam hal ini, komponen tambahan mesti diperkenalkan ke dalamnya). Kami menambah bahawa medan pusaran magnetik yang dibuat oleh arus yang bergerak dalam litar ditentukan dalam hal ini dengan mengambil kira arus bias, yang bergantung pada kadar perubahan aruhan elektrik.
Oleh itu, dalam praktiknya, di TOE, penyampaian formula untuk arus penuh dalam bentuk penjumlahan segmen kecil mikroskopik kontur dengan bidang eddy yang dibuat di dalamnya lebih popular. Pendekatan ini melibatkan penerapan persamaan Maxwell dalam bentuk integral. Ketika dilaksanakan, kontur dibagi menjadi segmen kecil, yang dianggap lurus pada perkiraan pertama (menurut hukum diasumsikan medan magnet seragam). Nilai ini, dilambangkan sebagai Um untuk satu bahagian diskrit panjang ΔL medan magnet yang bertindak dalam vakum, ditakrifkan sebagai berikut:
Um = HL * ΔL
Ketegangan total di sepanjang kontur L, yang disajikan secara ringkas dalam bentuk integral, dijumpai dengan formula berikut:
UL = Σ HL * ΔL.
Hukum jumlah arus untuk vakum
Dalam bentuk terakhirnya, yang disusun mengikut semua peraturan penyatuan, undang-undang jumlah arus seperti ini. Peredaran vektor "B" dalam gelung tertutup dapat ditunjukkan sebagai produk pemalar magnet m dalam jumlah arus:
Kamiran B over dL = kamiran Bl over dL = m In Di
di mana n ialah jumlah keseluruhan konduktor dengan arus pelbagai arah yang diliputi oleh litar L yang dibayangkan secara mental dari bentuk sewenang-wenangnya.
Setiap arus diambil kira dalam formula ini seberapa banyak yang diliputi sepenuhnya oleh litar ini.
Bentuk akhir pengiraan yang diperoleh untuk hukum arus total sangat dipengaruhi oleh media di mana daya elektromagnetik (medan) yang diinduksi bertindak.
Kesan alam sekitar
Hubungan yang dipertimbangkan untuk undang-undang arus dan medan tidak bertindak dalam keadaan hampa, tetapi dalam medium magnet, bentuknya sedikit berbeza. Dalam kes ini, sebagai tambahan kepada komponen arus utama, konsep arus mikroskopik yang timbul dalam magnet, misalnya, atau dalam bahan yang serupa dengannya, diperkenalkan.
Hubungan yang diperlukan berasal sepenuhnya dari teorema mengenai peredaran vektor aruhan magnetik B. Secara sederhana, ia dinyatakan dalam bentuk berikut. Nilai keseluruhan vektor B apabila disatukan di atas litar yang dipilih adalah sama dengan jumlah arus makro yang diliputi olehnya didarab dengan pekali pemalar magnet.
Akibatnya, formula untuk "B" dalam bahan ditentukan oleh ungkapan:
Kamiran B over dL = kamiran Bl over dL = m(Saya+Saya1)
di mana: dL adalah elemen diskrit litar di sepanjang pintasannya, Bl adalah komponen dalam arah tangen pada titik sewenang-wenang, bI dan I1 adalah arus konduksi dan arus mikroskopik (molekul).
Sekiranya ladang bertindak dalam persekitaran yang terdiri daripada bahan sewenang-wenangnya, arus mikroskopik ciri struktur ini harus diambil kira.
Pengiraan ini juga berlaku untuk medan yang dibuat di solenoid atau di media lain dengan kebolehtelapan magnet terhingga.
Untuk rujukan
Dalam sistem pengukuran GHS yang paling lengkap dan komprehensif, kekuatan medan magnet ditunjukkan dalam Oersteds (E). Dalam sistem lain yang ada (SI), dinyatakan dalam ampere per meter (A / meter). Hari ini, oersted secara beransur-ansur digantikan oleh unit yang lebih senang - ampere per meter.Semasa menerjemahkan hasil pengukuran atau pengiraan dari SI ke GHS, nisbah berikut digunakan:
1 e = 1000 / (4π) A / m ≈ 79.5775 ampere / meter.
Pada bahagian akhir tinjauan, kami perhatikan bahawa tidak kira apa kata undang-undang arus penuh digunakan, intinya tetap tidak berubah. Dengan kata-katanya sendiri, ini dapat dinyatakan sebagai berikut: ia menyatakan hubungan antara arus yang menembusi litar tertentu dan medan magnet yang dibuat dalam bahan.
Akhirnya, kami mengesyorkan menonton video yang berguna mengenai topik artikel:
Bahan berkaitan: