Undang-undang Pertama dan Kedua Kirchhoff - Penjelasan yang Mampu
Undang-undang pertama Kirchhoff
Definisi undang-undang pertama adalah: “Jumlah arus algebra yang mengalir melalui nod adalah sifar. " Anda boleh mengatakan bentuk yang sedikit berbeza: "Berapa banyak arus yang mengalir ke simpul, bilangan yang sama mengalir keluar, yang menunjukkan ketekalan arus ".
Simpul rantai adalah titik sambungan tiga atau lebih cabang. Arus dalam kes ini diedarkan mengikut tahap ketahanan setiap cabang.
Saya1= Saya2+ Saya3
Bentuk rakaman ini berlaku untuk litar DC. Sekiranya anda menggunakan undang-undang Kirchhoff pertama untuk litar arus bolak-balik, maka nilai voltan sesaat digunakan, dilambangkan dengan huruf İ dan ditulis dalam bentuk kompleks, dan kaedah pengiraannya tetap sama:
Bentuk kompleks mengambil kira komponen aktif dan reaktif.
Hukum Kedua Kirchhoff
Sekiranya yang pertama menggambarkan pengedaran arus di cabang, maka hukum Kirchhoff kedua adalah: "Jumlah penurunan voltan dalam litar sama dengan jumlah semua EMF. "Dengan kata mudah, kata-katanya berbunyi seperti berikut: “EMF yang diterapkan pada bahagian litar akan didistribusikan di antara elemen-elemen litar ini sesuai dengan rintangan, iaitu. mengikut undang-undang Ohm. "
Manakala untuk arus bolak-bunyinya seperti ini: "Jumlah amplitud EMF kompleks sama dengan jumlah penurunan voltan kompleks pada unsur-unsur ".
Z adalah impedans atau rintangan kompleks, ia merangkumi bahagian resistif dan reaktif (induktansi dan kapasitansi), yang bergantung pada frekuensi arus bolak-balik (dalam arus terus hanya ada rintangan aktif). Berikut adalah formula rintangan kapasitor dan aruhan yang kompleks:
Berikut adalah gambar yang menggambarkan perkara di atas:
Kemudian:
Kaedah pengiraan untuk undang-undang pertama dan kedua Kirchhoff
Mari kita praktikkan bahan teori. Untuk meletakkan tanda dalam persamaan dengan betul, anda perlu memilih arah litar. Lihat gambar rajah:
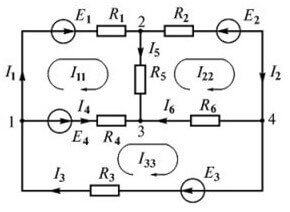
Kami mencadangkan memilih arah mengikut arah jam dan tandakan pada gambar:
Garis putus-putus menunjukkan cara mengikuti jalan ketika membuat persamaan.
Langkah seterusnya adalah menyusun persamaan mengikut undang-undang Kirchhoff. Pertama kita menggunakan yang kedua.Kami meletakkan tanda dengan cara ini: tanda tolak ditempatkan di depan kekuatan elektromotif jika diarahkan berlawanan arah jarum jam (arah yang kami pilih pada langkah sebelumnya), kemudian untuk arah jarum jam kami meletakkan tanda tolak. Kami menyusun untuk setiap litar, dengan mengambil kira tanda-tanda.
Untuk yang pertama, kita melihat arah EMF, bertepatan dengan garis putus-putus, set E1 plus E2:
Untuk yang kedua:
Untuk yang ketiga:
Tanda-tanda untuk IR (voltan) bergantung pada arah arus gelung. Di sini peraturan tanda sama seperti kes sebelumnya.
IR ditulis dengan tanda positif jika arus mengalir mengikut arah pintasan litar. Dan dengan tanda "-", jika arus mengalir melawan arah litar.
Arah lintasan litar adalah kuantiti bersyarat. Ia diperlukan hanya untuk susunan tanda dalam persamaan, ia dipilih secara sewenang-wenang dan tidak mempengaruhi ketepatan pengiraan. Dalam beberapa kes, arah pintasan yang tidak dipilih dapat menyukarkan pengiraan, tetapi ini tidak penting.
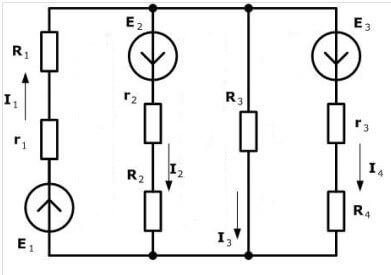
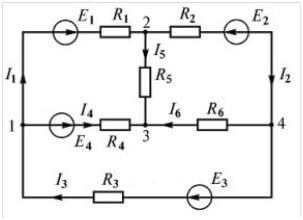
Pertimbangkan litar lain:
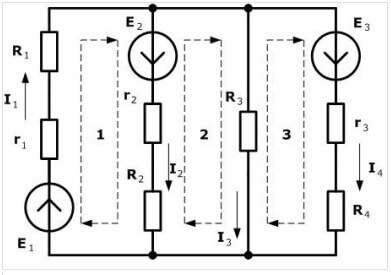
Terdapat sebanyak empat sumber EMF, tetapi prosedur pengiraannya sama, pertama kita memilih arah untuk membuat persamaan.
Sekarang anda perlu membuat persamaan mengikut undang-undang pertama Kirchhoff. Untuk simpul pertama (rajah 1 di sebelah kiri rajah):
Saya3 mengalir masuk, dan saya1, Saya4 ia mengikuti, maka tanda-tandanya. Untuk yang kedua:
Untuk yang ketiga:
Soalan: "Terdapat empat simpul, dan hanya ada tiga persamaan, mengapa? "Faktanya ialah bilangan persamaan peraturan Kirchhoff pertama sama dengan:
Npersamaan= nsimpulan-1
I.E. hanya ada 1 persamaan yang lebih sedikit daripada nod, kerana ini cukup untuk menggambarkan arus di semua cabang, saya menasihatkan sekali lagi untuk naik ke litar dan periksa sama ada semua arus ditulis dalam persamaan.
Sekarang kita meneruskan pembinaan persamaan dengan peraturan kedua. Untuk litar utama:
Untuk litar kedua:
Untuk litar ketiga:
Sekiranya kita mengganti nilai voltan dan rintangan sebenar, maka ternyata undang-undang pertama dan kedua adalah adil dan dipenuhi. Ini adalah contoh mudah; dalam praktiknya, masalah yang lebih besar harus diselesaikan.
Kesimpulannya. Perkara utama semasa mengira dengan bantuan undang-undang Kirchhoff pertama dan kedua adalah pematuhan peraturan untuk membuat persamaan, iaitu. mengambil kira arah aliran arus dan pintasan litar untuk susunan tanda yang betul bagi setiap elemen litar.
Hukum Kirchhoff untuk litar magnet
Pengiraan litar magnetik juga penting dalam kejuruteraan elektrik, kedua-dua undang-undang telah menemui penerapannya di sini. Intinya tetap sama, tetapi jenis dan saiznya berubah, mari kita lihat masalah ini dengan lebih terperinci. Mula-mula anda perlu menangani konsep.
Magnetomotive force (MDS) ditentukan oleh produk dari jumlah putaran gegelung, oleh arus yang melaluinya:
F = w * i
Voltan magnetik adalah produk kekuatan medan magnet dan arus melalui bahagian, yang diukur dalam Amperes:
Um= H * Saya
Atau fluks magnet melalui rintangan magnetik:
Um= F * Rm
L adalah panjang purata plot, μr dan μ0 - kebolehtelapan magnet relatif dan mutlak.
Dengan membuat analogi, kami menulis undang-undang Kirchhoff pertama untuk litar magnet:
Iaitu, jumlah semua fluks magnetik melalui nod adalah sifar. Pernahkah anda perhatikan bahawa bunyinya hampir sama dengan litar elektrik?
Kemudian undang-undang Kirchhoff kedua terdengar seperti "Jumlah MDS dalam litar magnet sama dengan jumlah UM (tekanan magnetik).
Fluks magnet sama dengan:
Untuk medan magnet bergantian:
Ia hanya bergantung pada voltan melintasi belitan, dan bukan pada parameter litar magnet.
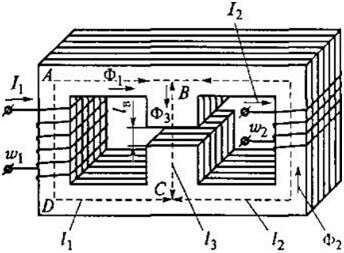
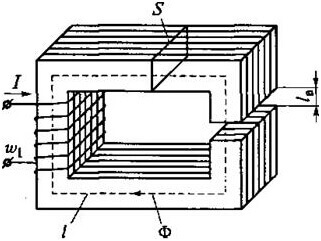
Sebagai contoh, pertimbangkan kontur ini:
Kemudian untuk ABCD kami mendapat formula berikut:
Untuk litar dengan jurang udara, hubungan berikut adalah benar:
Rintangan Magnetik:
Dan rintangan jurang udara (di sebelah kanan di teras):
Di mana S adalah kawasan teras.
Untuk memahami sepenuhnya bahan dan mengkaji secara visual beberapa nuansa penggunaan peraturan, kami mengesyorkan agar anda membiasakan diri dengan kuliah yang disediakan di video:
Penemuan Gustav Kirchhoff memberikan sumbangan yang besar terhadap perkembangan sains, terutamanya kejuruteraan elektrik.Dengan bantuan mereka, cukup mudah untuk mengira litar elektrik atau magnetik, arus di dalamnya dan voltan. Kami berharap sekarang peraturan Kirchhoff untuk litar elektrik dan magnet menjadi lebih jelas bagi anda.
Bahan serupa:

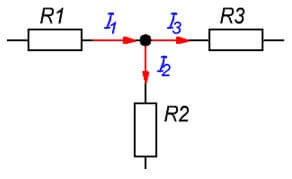
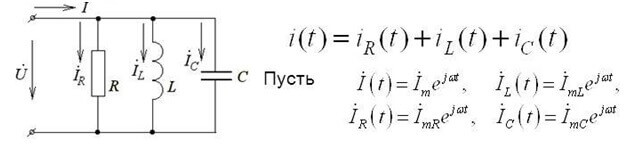
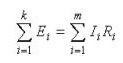
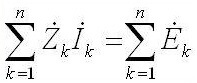
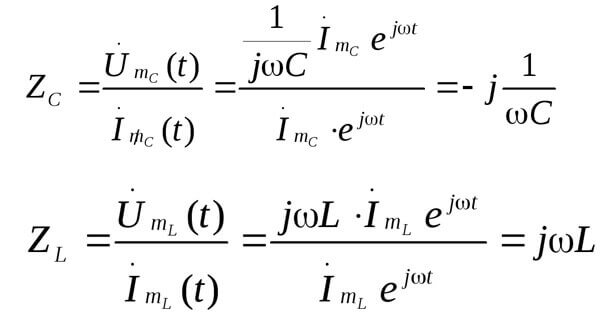

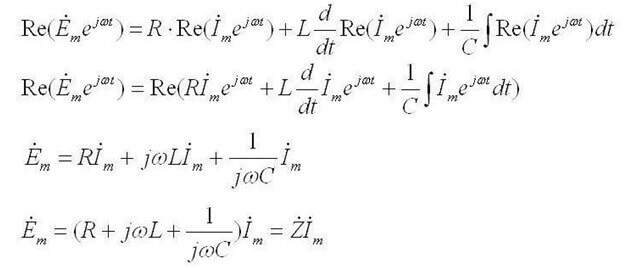
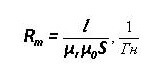
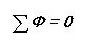
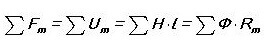
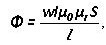
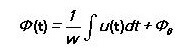
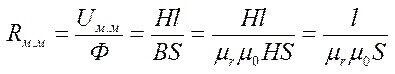
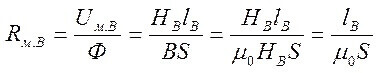


Apabila kita menyusun uru menurut undang-undang Kirchhoff 1, iaitu penjelasan yang baik mengenai ur pertama. Mengapa tidak ada penjelasan untuk yang kedua dan ketiga, ketika semuanya lebih jelas di sana? I2 jelas mengalir ke sana, tetapi untuk sebab tertentu dia mempunyai tanda positif
dalam persamaan ketiga, jadi secara amnya ketiga-tiga saya mengalir masuk. Mengapa mereka positif?
Harap maklum bahawa pada awal artikel, persamaan dianggap dalam bentuk I1 = I2 + I3, jika anda memindahkan semuanya ke sebelah kiri persamaan, I1-I2-I3 = 0. Perkara yang sama dilakukan di sana.
Untuk nod kedua:
I1 = I5 + I2
menggerakkan semuanya ke satu arah akan keluar:
I1-I5-I2 = 0
Membandingkan dengan arah pintasan litar, akan menjadi jelas bahawa lebih baik menukar tanda, iaitu, kalikan dengan tolak 1.
Akan keluar
-I1 + I5 + I2 = 0
yang setara
I2 + I5-I1 = 0