A teljes áram törvénye egyszerű szavakkal
A villamosmérnöki nevű ismerős tárgy a programjában alapvető törvények sorozatát tartalmazza, amelyek meghatározzák a mágneses mező fizikai kölcsönhatásának alapelveit. Meghosszabbítják hatásukat az elektromos készülékek különféle elemeire, valamint szerkezetükre és környezetükre. Az azokban zajló folyamatok fizikája olyan alapfogalmakra vonatkozik, mint a villamos áram és a mezők. A teljes áram törvénye határozza meg az elektromos töltések mozgása és az általa létrehozott mágneses mező (pontosabban annak intenzitása) kapcsolatát. A modern tudomány azt állítja, hogy alkalmazása szinte minden környezetre kiterjed.
A törvény lényege
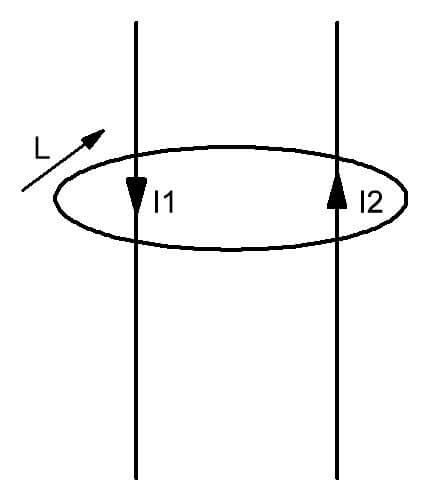
A mágneses áramkörökre alkalmazandó mérlegelhető törvény meghatározza az alkotóelemek közötti következő mennyiségi kapcsolatot. A mágneses mező vektor keringése zárt hurokban arányos a rajta áthatoló áramok összegével. A teljes áram törvény fizikai jelentésének megértése érdekében meg kell ismerkednie az általa leírt folyamatok grafikus ábrázolásával.
Az ábrából kitűnik, hogy körülbelül két olyan vezetővel, amelyekben az I1 és I2 áramok átfolynak, egy mezőt képez, amelyet az L áramkör korlátoz. Ez egy szellemileg elképzelt zárt ábra, amelynek síkját mozgó töltésű vezetők átszúrják. Egyszerű szavakkal ez a törvény a következőképpen fejezhető ki. Ha az L áramkör által lefedett képzeletbeli képzeletbeli felületen több villamos áram folyik, akkor egy adott feszültség-eloszlású mágneses mező jön létre.
A vektor pozitív irányához a mágneses áramkör kontúrjára vonatkozó törvénynek megfelelően az óramutató járásával megegyezően kerül kiválasztásra. Ez is elképzelhető.
Az áramlás által létrehozott örvénymező ilyen meghatározása azt sugallja, hogy az áramok iránya tetszőleges lehet.
Referenciaként! A bevezetett mezőszerkezetet és az azt leíró készüléket meg kell különböztetni az „E” elektrosztatikus vektor keringésétől, amely mindig egyenlő az áramkört meghaladó nullával. Ennek eredményeként egy ilyen mező a potenciális struktúrákra utal. A mágneses mező „B” vektorának keringése soha nem lehet nulla. Ezért hívják „örvénynek”.
Alapfogalmak
A vizsgált törvénynek megfelelően a következő egyszerűsített megközelítést kell használni a mágneses mezők kiszámításához. A teljes áramot egy zárt L áramkör által lefedett felületen átfolyó több elem összegeként ábrázoljuk. Az elméleti számításokat a következőképpen lehet bemutatni:
- Az uits I körökön átmenő teljes elektromos áram az I1 és I2 vektorösszege.
- Ebben a példában annak meghatározásához használja a következő képletet:
ΣI = I1 - I2 (mínusz a második kifejezés előtt azt jelenti, hogy az áramok iránya ellentétes). - Ezeket viszont az elektrotechnikában ismert törvény (szabály) szerint határozzák meg. átfúr.
A kontúr mentén mágneses teret a speciális technikákkal kapott számítások alapján számítják ki. Ennek megtalálásához integrálni kell ezt a paramétert az L felett, az egyik formában bemutatott Maxwell-egyenlet felhasználásával.Különböző formában alkalmazható, de ez némileg bonyolítja a számításokat.
Egyszerűsített integrált megközelítés
Ha differenciális ábrázolást alkalmazunk, akkor a teljes áram törvényének egyszerűsített formában történő kifejezése nagyon nehéz lesz (ebben az esetben kiegészítő elemeket kell bevezetni). Ehhez hozzátesszük, hogy az áramkörön belül mozgó áramok által létrehozott mágneses örvényteret ebben az esetben meghatározzuk, figyelembe véve a torzítóáramot, amely az elektromos indukció változásának sebességétől függ.
Ezért a gyakorlatban a TOE-ban népszerűbb a teljes áramok képleteinek bemutatása egy áramkör mikroszkopikusan kis szegmenseinek összegzése formájában, azokban létrehozott örvény mezőkkel. Ez a megközelítés magában foglalja a Maxwell-egyenlet integrált formában történő alkalmazását. Végrehajtásakor a kontúr kisméretű részekre oszlik, amelyeket az első közelítésben egyértelműnek tekintnek (a törvény szerint feltételezzük, hogy a mágneses mező homogén). Ezt az értéket, amelyet Um-vel jelölnek a vákuumban működő mágneses mező egy ΔL hosszúságú különálló szakaszára, a következőképpen kell meghatározni:
Um = HL * ΔL
Az L teljes kontúr mentén mutatott teljes feszültséget, amelyet röviden integrált formában mutatunk be, a következő képlet határozza meg:
UL = Σ HL * ΔL.
A vákuum teljes áramának törvénye
Végső formájában, az integrációs szabályok szerint, a teljes áram törvénye így néz ki. A "B" vektor keringésének zárt hurokban a mágneses állandó szorzata lehet m az áramok mennyiségében:
A B integrálja dL felett = Bl integrálja dL = felett m Σ Be
ahol n a többirányú árammal rendelkező vezetők teljes száma, amelyet egy önkényes alakú mentálisan képzelhető L áramkör fed le.
Ebben a képletben minden áramot annyiszor vesszük figyelembe, amennyire ez az áramkör teljesen lefedi.
A teljes áram törvényére vonatkozó számítások végső formáját nagyban befolyásolja az a közeg, amelyben az indukált elektromágneses erő (mező) működik.
Környezeti hatás
A nem vákuumban, hanem mágneses közegben működő áramok és mezők törvényi viszonyai kissé eltérő formában alakulnak ki. Ebben az esetben a fő áramkomponenseken kívül bevezetik például a mágnesben vagy a hozzá hasonló anyagban keletkező mikroszkopikus áramok fogalmát.
A szükséges összefüggést teljes egészében a B mágneses indukció vektorkeringetéséről szóló tétel határozza meg. Egyszerűen fogalmazva, a következő formában fejezzük ki. A kiválasztott áramkörbe integrálva a B vektor teljes értéke megegyezik az által lefedett makroáramok összegével, szorozva a mágneses állandó koefficienssel.
Ennek eredményeként az anyagban a „B” képletet a következő kifejezés határozza meg:
A B integrálja dL felett = Bl integrálja dL = felett m(én+én1)
ahol: dL az áramkör diszkrét eleme, amely a megkerülő út mentén irányul, Bl az összetevő az érintő irányában egy tetszőleges ponton, bI és I1 a vezetőképesség és a mikroszkopikus (molekuláris) áram.
Ha a mező tetszőleges anyagokból álló környezetben működik, akkor figyelembe kell venni az ezekre a struktúrákra jellemző mikroszkopikus áramokat.
Ezek a számítások igazak a mágnesszelepen vagy bármely más, véges mágneses permeabilitással rendelkező közegben létrehozott mezőre is.
Referenciaként
A GHS legteljesebb és legátfogóbb mérési rendszerében a mágneses térerősség Oersteds-ben (E) látható. Egy másik létező rendszerben (SI) azt méter amperben (A / méter) fejezik ki. Manapság az oersted-t fokozatosan felváltja egy működőképesebb egység - egy méterre eső amper.A mérések vagy számítások eredményeinek SI-ről GHS-re történő lefordításakor a következő arányt kell használni:
1 E = 1000 / (4π) A / m ≈ 79,5775 Ampere / méter.
A felülvizsgálat utolsó részében megjegyezzük, hogy a teljes áramerősség törvényének megfogalmazásától függetlenül annak lényege változatlan marad. Saját szavai szerint ez a következőképpen reprezentálható: kifejezi az adott áramkörbe behatoló áramok és az anyagban létrehozott mágneses mezők kapcsolatát.
Végül azt javasoljuk, hogy nézzen meg egy hasznos videót a cikk témájáról:
Kapcsolódó anyagok: