Kirchhoff első és második törvénye - megfizethető magyarázat
Kirchhoff első törvénye
Az első törvény meghatározása a következő:A csomóponton átfolyó áramok algebrai összege nulla. ” Megmondhatja egy kicsit más formát: "Hány áram áramolt a csomópontba, ugyanaz a szám áramlott ki, ami az áram állandóságát jelzi ”.
A lánc csomópontja három vagy több ág csatlakozási pontja. A áramok ebben az esetben az egyes ágok ellenállásával arányosan oszlanak meg.
én1= Én2+ Én3
Ez a felvételi forma DC áramkörökre érvényes. Ha az első Kirchhoff-törvényt alkalmazzuk egy váltakozó áramú áramkörre, akkor a pillanatnyi feszültségértékeket İ betűvel jelöljük és összetett formában írjuk, és a számítási módszer ugyanaz marad:
A komplex forma figyelembe veszi mind az aktív, mind a reaktív komponenseket.
Kirchhoff második törvény
Ha az első leírja az áramok eloszlását az ágakban, akkor a második Kirchhoff-törvény a következő:Az áramkörben a feszültségcsökkenések összege megegyezik az összes EMF összegével. ”Egyszerű szavakkal: a megfogalmazás a következő: Ohm törvénye szerint. "
Míg a váltakozó áram esetében ez így hangzik: “A komplex EMF amplitúdóinak összege megegyezik az elemekre eső komplex feszültség csökkenésének összegével ".
Z az impedancia vagy komplex ellenállás, magában foglalja mind az ellenállást, mind a reaktív részt (induktivitás és kapacitás), amely a váltakozó áram frekvenciájától függ (egyenáramban csak aktív ellenállás van). Az alábbiakban a kondenzátor komplex ellenállásának és az induktivitásnak a képleteit mutatjuk be:
Íme egy kép a fentiekről:
majd:
Számítási módszerek Kirchhoff első és második törvényére
Menjünk az elméleti anyag gyakorlati megvalósításához. A jelek helyes elhelyezéséhez az egyenletben ki kell választania az áramkör irányát. Vessen egy pillantást a diagramra:
Javasoljuk, hogy válassza az óramutató járásával megegyező irányba, és jelölje meg az ábrán:
A szaggatott vonal jelzi, hogyan kell követni az utat egyenletek elkészítésekor.
A következő lépés az egyenletek Kirchhoff törvényei szerinti összeállítása. Először a másodikt használjuk.Így tesszük a jeleket: mínuszjelet helyezünk az elektromos erő elé, ha az óramutató járásával ellentétesen van (az előző lépésben kiválasztott irány), akkor az óramutató járásával megegyező irányban az mínuszjelet helyezzük el. Minden áramkört összeállítunk, figyelembe véve a jeleket.
Először az EML irányát nézzük, ez egybeesik a kötőjel-pontozott vonallal, E1 plusz E2:
A második:
A harmadik:
Az IR (feszültség) jelei a hurokáramok irányától függenek. Itt a jelszabály ugyanaz, mint az előző esetben.
Az IR pozitív jellel íródik, ha az áram az áramkör bypass irányában áramlik. És „-” jelzéssel, ha az áram az áramkör irányával szemben áramlik.
Az áramlás iránya egy feltételes mennyiség. Csak a jelek egyenletekben történő elrendezésére van szükség, önkényesen választják, és nem befolyásolja a számítások helyességét. Bizonyos esetekben a rosszul megválasztott megkerülési irány bonyolíthatja a számítást, de ez nem kritikus.
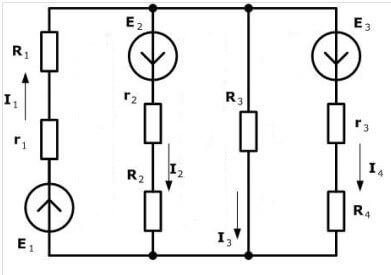
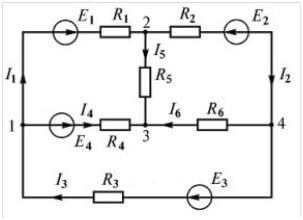
Vegyünk egy másik áramkört:
Négy EMF-forrás van, de a számítási eljárás ugyanaz, először az egyenletek elkészítésének irányát választjuk meg.
Most ki kell állítania az egyenleteket a Kirchhoff első törvényének megfelelően. Az első csomópontra (1. ábra a diagram bal oldalán):
én3 beáramlik, és én1, Én4 ebből következik, tehát a jelek. A második:
A harmadik:
Kérdés: "Négy csomópont van, és csak három egyenlet létezik, miért? "A tény az, hogy az első Kirchhoff-szabály egyenleteinek száma egyenlő:
Negyenletek= ncsomós-1
Ie csak 1 kevesebb egyenlet van, mint a csomópontoknak, mert ez elegendő az összes ág áramlásának leírására, javaslom még egyszer menjen fel az áramkörre, és ellenőrizze, hogy az összes áram meg van-e írva az egyenletekben.
Most tovább lépünk az egyenletek konstruálására a második szabály szerint. Az elsődleges áramkörnél:
A második áramkörnél:
A harmadik áramkörnél:
Ha a valós feszültség és ellenállás értékeit cseréljük ki, akkor kiderül, hogy az első és a második törvény tisztességes és teljesül. Ezek egyszerű példák, a gyakorlatban sokkal nagyobb problémákat kell megoldani.
következtetés. Az első és a második Kirchhoff-törvény segítségével történő számítás során a fő dolog az egyenletek meghatározására vonatkozó szabály betartása, azaz vegye figyelembe az áramáram irányát és az áramkör megkerülését a jelek helyes elrendezéséhez az áramkör egyes elemeihez.
Kirchhoff mágneses áramkörének törvényei
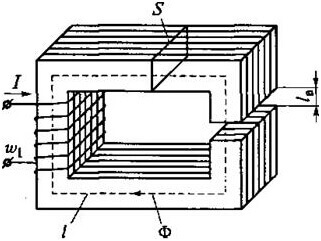
A mágneses áramkörök számításai szintén fontosak az elektrotechnikában, mindkét törvény alkalmazta itt. A lényeg változatlan marad, de a típus és a méret megváltozik, nézzük meg részletesebben ezt a kérdést. Először foglalkoznia kell a fogalmakkal.
A mágneses erőt (MDS) a tekercs fordulásainak szorzata, a rajta átmenő áram szorzata határozza meg:
F = w * i
A mágneses feszültség a mágneses térerősség és a szakaszon átáramló áram szorzata, amperben mérve:
Um= H * I
Vagy mágneses fluxus mágneses ellenállás révén:
Um= F * Rm
L a grafikon átlagos hossza, μr és μ0 - relatív és abszolút mágneses permeabilitás.
Analógiát felhívva írjuk az első Kirchhoff-törvényt egy mágneses áramkörre:
Vagyis a csomóponton keresztüli összes mágneses fluxus összege nulla. Észrevetted, hogy ez úgy hangzik, mintha egy elektromos áramkör lenne?
Akkor Kirchhoff második törvénye így hangzik: „A mágneses áramkörben az MDS összege egyenlő az U összeggelM (mágneses feszültség).
A mágneses fluxus egyenlő:
Váltakozó mágneses mező esetén:
Ez csak a tekercs feszültségétől függ, és nem a mágneses áramkör paramétereitől.
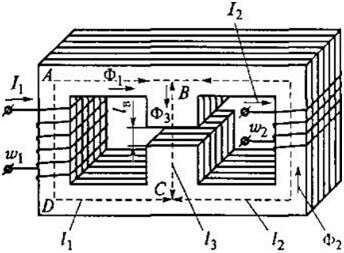
Példaként vegye figyelembe ezt a körvonalat:
Aztán az ABCD-hez a következő képletet kapjuk:
Légrésű áramköröknél a következő kapcsolatok igazak:
Mágneses ellenállás:
És a légrés ellenállása (a mag jobb oldalán):
Ahol S a központi terület.
Az anyag teljes megértése és a szabályok alkalmazásának néhány árnyalata vizuális áttekintése érdekében javasoljuk, hogy ismerkedjen meg a videóban található előadásokkal:
Gustav Kirchhoff felfedezései jelentős mértékben hozzájárultak a tudomány fejlődéséhez, különös tekintettel az elektrotechnikára.Ezek segítségével meglehetősen egyszerű kiszámítani az elektromos vagy mágneses áramkört, az abban lévő áramokat és a feszültségeket. Reméljük, hogy most Kirchhoff elektromos és mágneses áramkörökre vonatkozó szabályai világosabbá válnak számodra.
Hasonló anyagok:

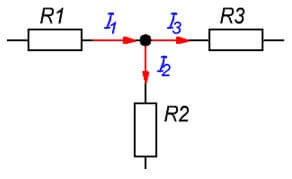
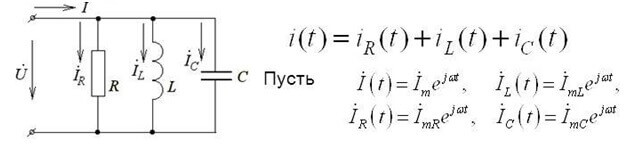
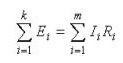
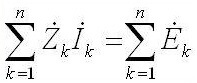
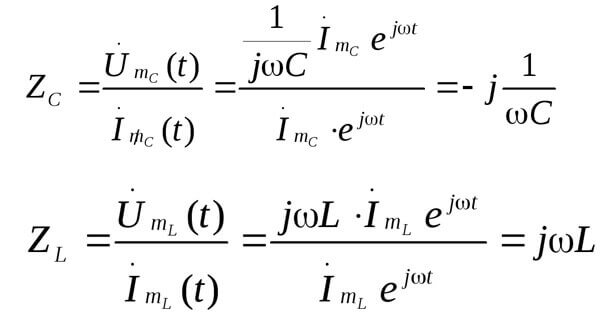

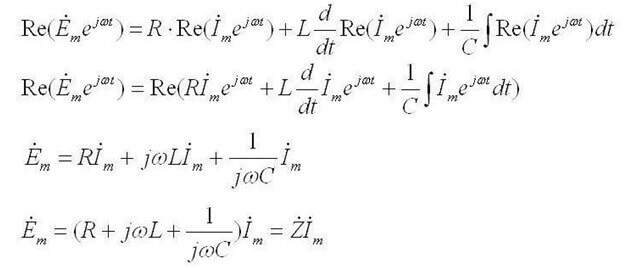
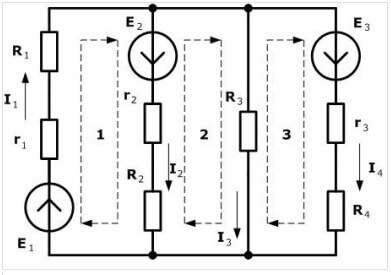
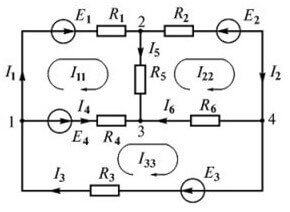
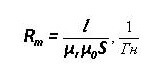
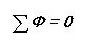
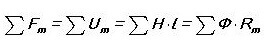
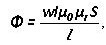
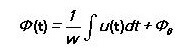
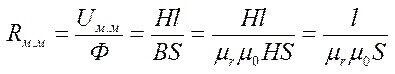
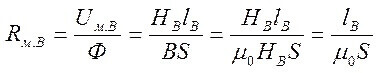


Amikor Kirchhoff első törvényének megfelelően ur-et állítunk össze, azaz az első ur jó magyarázata. Miért nem magyarázható a második és a harmadik, amikor ott minden sokkal homályosabb? Az I2 egyértelműen ott áramlik, de valamilyen okból pozitív jele van
a harmadik egyenletben, tehát általában mindhárom beáramlok. Miért pozitívak?
Felhívjuk figyelmét, hogy a cikk elején az egyenletet I1 = I2 + I3 formában tekintjük, ha mindent átvisszünk az egyenlet bal oldalára, I1-I2-I3 = 0. Ugyanez történt ott.
A második csomóponthoz:
I1 = I5 + I2
mindent egy irányba mozgatva kiderül:
I1-I5-I2 = 0
Az áramkör megkerülésének irányával összehasonlítva világossá válik, hogy jobb a jeleket megváltoztatni, vagyis szorozni mínusz 1-sel.
Ki fog jönni
-I1 + I5 + I2 = 0
ami egyenértékű
I2 + I5-I1 = 0