Hogyan lehet megtalálni az áram erősségét?

Az elektromos áramkör egyik fő jellemzője az áram. A mérés amperben történik, és meghatározza a vezető huzalok, gumiabroncsok vagy áramköri táblák terhelését. Ez az érték tükrözi a villamosenergia mennyiségét, amely időegységben áramlik a vezetőben. Számos módja van annak meghatározására, az ismeretektől függően. Ennek megfelelően a hallgatók és a kezdő villanyszerelők ezért gyakran tapasztalnak problémákat oktatási feladatok vagy gyakorlati helyzetek megoldásakor. Ebben a cikkben elmondjuk, hogyan lehet megtalálni az áram erősségét feszültség vagy feszültség vagy ellenállás révén.

Tartalom:

Ha az energia és a feszültség ismert
Ha ismert feszültség vagy teljesítmény és ellenállás
Ha EMF, akkor a belső ellenállás és a terhelés ismert
Joule-Lenz törvény
Néhány példa

Ha az energia és a feszültség ismert

Tegyük fel, hogy meg kell találnia az áramkör erősségét, miközben csak a feszültséget és az energiafogyasztást ismeri. Ezután ellenállás nélkül történő meghatározásához használja a következő képletet:

P = UI

Az egyszerűség után megkapjuk a számítási képletet

I = P / U

Meg kell jegyezni, hogy ez a kifejezés DC áramkörökre érvényes. De például a villamos motorok számításánál a teljes teljesítményt vagy a koszinusz Phi-t veszik figyelembe. Ezután egy háromfázisú motorhoz a következőképpen lehet kiszámítani:

Azt találjuk, hogy a P figyelembe veszi a hatékonyságot, általában 0,75–0,88 tartományban van:

P1 = P2 / η

Itt P2 az aktív nettó teljesítmény a tengelyen, η - hatékonyság,mindkét paraméter általában az adattáblát jelzi.

A teljes energiát a cosФ figyelembevételével találjuk meg (az adattáblán is szerepel):

S = P1 / cosφ

Az aktuális fogyasztást a következő képlet alapján határozhatjuk meg:

Inom = S / (1,73 · U)

Itt 1,73 a 3 gyökere (a háromfázisú áramkör kiszámításához), U a feszültség, a bekapcsolt motortól (háromszög vagy csillag) és a hálózat feszültségeinek számától (220, 380, 660 stb.) Függ. Bár hazánkban a 380 V-ot gyakran találják meg.

Ha ismert feszültség vagy teljesítmény és ellenállás

Problémák vannak azonban akkor, ha ismeri az áramkör feszültségét és a terhelés nagyságát, majd áramfelvétel nélkül keresheti meg az áramot Ohm törvényesegítségével segítségével kiszámoljuk az áramerősséget az ellenállás és a feszültség alapján.

I = U / R

De néha előfordul, hogy meg kell határoznia az áramerősséget feszültség nélkül, vagyis amikor csak az áramkör teljesítményét és ellenállását ismeri. Ebben az esetben:

P = UI

Sőt, Ohm ugyanazon törvénye szerint:

U = IR

Hogy:

P = i²* R

A számítást tehát a képlet szerint hajtjuk végre:

én²= P / R

Vagy vegye a kifejezés jobb oldalán található kifejezést a gyökér alatt:

I = (P / R)^1/2

Ha EMF, akkor a belső ellenállás és a terhelés ismert

A fogással kapcsolatos hallgatói problémák esetén vannak olyan esetek, amikor megkapják az EML nagyságát és az áramforrás belső ellenállását. Ebben az esetben a teljes áramkör Ohm törvénye alapján meghatározhatja az áramkör erősségét:

I = E / (R + r)

Itt E az EMF, r az áramforrás belső ellenállása és R a terhelés.

Joule-Lenz törvény

Egy másik feladat, amely még egy többé-kevésbé tapasztalt hallgatónak is belemerülhet a sztúrába, az áram erősségének meghatározása, ha az idő, az ellenállás és a vezető által kibocsátott hőmennyiség ismert.Erre emlékeztetünk Joule-Lenz törvény.

Formula így néz ki:

Q = I²Rt

Ezután végezze el a számítást az alábbiak szerint:

én²= QRt

Vagy adja hozzá az egyenlet jobb oldalát a gyökér alá:

I = (Q / Rt)^1/2

Néhány példa

Következésképpen azt javasoljuk, hogy a kapott információkat rögzítse több olyan feladat példáján, amelyekben meg kell találni az aktuális erősséget.

1 feladat: Számítsuk ki az I ellenállást két sorozatú és párhuzamos csatlakozás ellenállásában. 1. és 2. ohm R ellenállás, 12 voltos tápegység.

A feltétel alapján egyértelmű, hogy a vegyületek mindegyik változatára két választ kell adnia. Ezután az áramerősség soros csatlakozásban történő megtalálásához először összeadja az áramkör ellenállását, hogy megkapja a teljes értéket.

R₁+ R₂= 1 + 2 = 3 Ohm

Ezután kiszámíthatja az aktuális erőt Ohm törvénye szerint:

I = U / R = 12/3 = 4 amper

Két elem párhuzamos csatlakoztatásával az Rtotal a következőképpen számítható ki:

Rtotal = (R1 * R2) / (R1 + R2) = 1 * 2/3 = 2/3 = 0,67

Ezután további számításokat hajthatunk végre az alábbiak szerint:

I = 12 * 0,67 = 18A

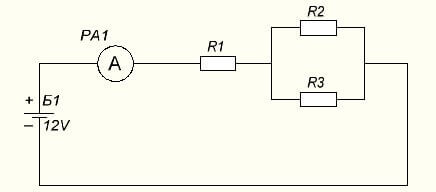
2 feladat: számítsa ki az elemek vegyes csatlakoztatásának áramát. A tápegység kimenete 24 V, az ellenállások: R1 = 1 Ohm, R2 = 3 Ohm, R3 = 3 Ohm.

Mindenekelőtt meg kell találnunk az R összes értékét párhuzamosan kapcsolt R2-ben és R3-ban, ugyanazon képlet szerint, amelyet fent használtunk.

Rpriv = (R2 * R3) / (R2 + R3) = (3 * 3) | (3 + 3) = 9/6 = 3/2 = 1,5 Ohm

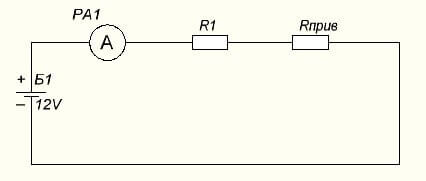
Az áramkör mostantól a következőképpen alakul:

Ezután ugyanazon Ohm törvénye szerint találjuk meg az áramot:

I = U / (R1 + Rpriv) = 24 / (1 + 1,5) = 24 / 2,5 = 9,6 amper

Most már tudja, hogyan kell megtalálni az áramerősséget, ismerve az erőt, az ellenállást és a feszültséget. Reméljük, hogy a megadott képletek és számítási példák segítettek megtanulni az anyagot!

Bizonyára nem tudod: