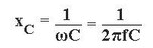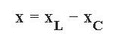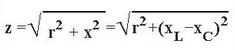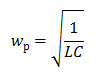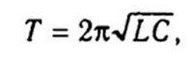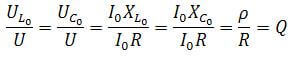Mi az áramok és a feszültségek rezonanciája?
Induktív reaktancia és kapacitás
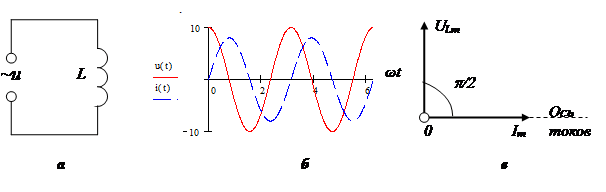
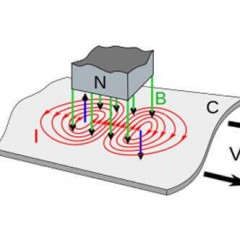
Az induktivitás a test azon képessége, hogy felhalmozzon energiát egy mágneses mezőben. Jellemzője a fázisban levő feszültségtől származó késés. Jellemző induktív elemek a fojtók, tekercsek, transzformátorok, villamos motorok.
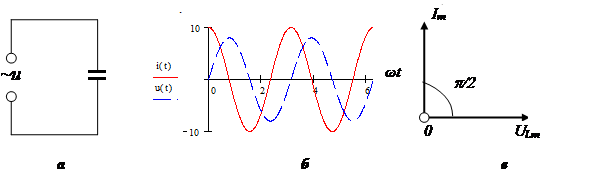
A kapacitás olyan elemekre utal, amelyek energiát tárolnak egy elektromos mezőn keresztül. A kapacitív elemeket az áram feszültségének fáziskésleltetése jellemzi. Kapacitív elemek: kondenzátorok, varicák.
Alapvető tulajdonságaikat megadják, a cikkben szereplő árnyalatokat nem veszik figyelembe.
A felsorolt elemek mellett másoknak is van bizonyos induktivitása és kapacitása, például az elektromos kábelek hosszában elosztva.
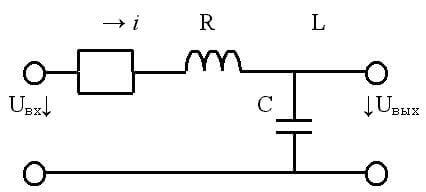
Kapacitás és induktivitás váltakozó áramú áramkörben
Ha az egyenáramú áramkörökben a kapacitás általában az áramkör szakadt része, és az induktivitás egy vezető, akkor váltakozó kondenzátorokban és tekercsekben az ellenállás reaktív analógja van.
Az induktor reaktanciáját a következő képlet határozza meg:
Vektoros ábra:
Kondenzátor reaktancia:
Itt w a szögfrekvencia, f a szinuszos áramkör frekvenciája, L az induktivitás, C a kapacitás.
Vektoros ábra:
Érdemes megjegyezni, hogy a sorba kapcsolt reaktív elemek kiszámításához a következő képletet kell használni:
Felhívjuk figyelmét, hogy a kapacitív komponenst mínuszjelet vesszük. Ha az aktív komponens (ellenállás) szintén jelen van az áramkörben, akkor a Pythagorai tétel képletének megfelelően (a vektordiagram alapján) adjuk hozzá:
Mire múlik a reaktancia? A reaktív jellemzők a kapacitás vagy induktivitás értékétől, valamint a váltakozó áram frekvenciájától függenek.
Ha megnézzük a reaktív komponens képletet, láthatjuk, hogy a kapacitív vagy induktív komponens bizonyos értékeinek különbsége nulla, akkor csak az ellenállás marad az áramkörben. De ezek nem minden jellemzője egy ilyen helyzetnek.
Feszültség rezonancia
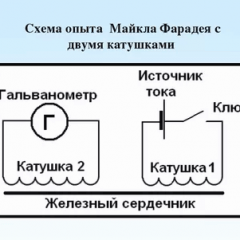
Ha a kondenzátort és az induktorokat sorosan összekapcsoljuk egy generátorral, akkor feltéve, hogy a reakcióképességük egyenlő, feszültség-rezonancia lép fel. Ebben az esetben a Z aktív résznek a lehető legkisebbnek kell lennie.
Érdemes megjegyezni, hogy az induktivitásnak és a kapacitásnak csak az idealizált példákban csak reaktív tulajdonságai vannak. A valódi áramkörökben és elemekben a vezetők aktív ellenállása mindig jelen van, bár ez rendkívül kicsi.
Rezonancia esetén energiacserélés történik az induktor és a kondenzátor között. Ideális példákban egy energiaforrás (generátor) kezdeti csatlakoztatása során az energia felhalmozódik a kondenzátorban (vagy induktorban), és kikapcsolása után ennek az átváltásnak köszönhetően laza oszcillációk fordulnak elő.
A fojtók feszültségei és a kapacitások kb Ohm törvénye:
U = I / X
Ahol X az Xc kapacitív vagy XL induktivitás.
Az induktivitásból és a kapacitásból álló áramkört oszcillációs áramkörnek nevezzük. Ennek gyakoriságát a következő képlettel kell kiszámítani:
Az oszcillációs periódust a Thompson képlet határozza meg:
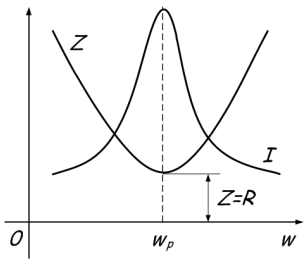
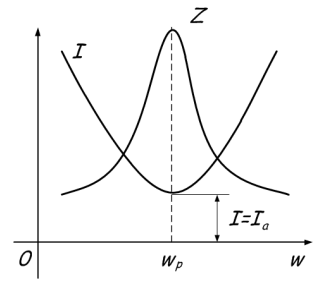
Mivel a reaktancia függ a frekvenciától, az induktivitási ellenállás a frekvencia növekedésével növekszik, és a kapacitással csökken. Ha az ellenállások azonosak, a teljes ellenállás nagymértékben csökken, ami a grafikonon tükröződik:
Az áramkör fő jellemzői a minőségi tényező (Q) és a frekvencia. Ha az áramkört négycsatlakozónak tekintjük, akkor annak átviteli együtthatója az egyszerű számítások után a minőségi tényezőre csökken:
K = q
És az áramkör kivezetésein a feszültség az áram átviteli együtthatójával (minőségi tényezőjével) növekszik.
UK = Uin * Q
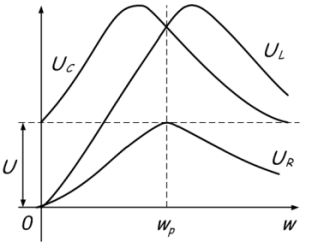
A feszültség-rezonancia esetén minél magasabb a minőségi tényező, annál nagyobb az áramköri elemek feszültsége meghaladja a csatlakoztatott generátor feszültségét. A feszültség tíz vagy százszor megnőhet. Ez a grafikonon látható:
Az áramkimaradások az áramkörben csak az aktív ellenállás jelenlétének tudhatók be. Az energiaforrásból származó energiát csak az ingadozások fenntartására veszik.
A teljesítménytényező egyenlő:
cosФ = 1
Ez a képlet azt mutatja, hogy veszteségek merülnek fel az aktív teljesítmény miatt:
S = P / Cosph
Rezonanciaáramok
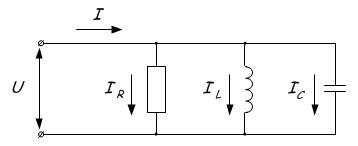
Az áram-rezonanciát azokban az áramkörökben figyeljük meg, ahol az induktivitás és a kapacitás párhuzamosan kapcsolódik.
A jelenség abban áll, hogy a kondenzátor és a tekercs között nagy áramok áramlik nulla áram mellett az áramkör el nem ágazott részén. Ennek oka az, hogy amikor a rezonancia frekvenciát elérték, a teljes Z ellenállás növekszik. Vagy egyszerűen szólva, így hangzik - a rezonancia pontnál eléri a Z ellenállás maximális összértékét, amely után az egyik ellenállás növekszik, a másik pedig csökken, attól függően, hogy a frekvencia növekszik vagy csökken. Ez grafikusan jelenik meg:
Általában minden hasonló az előző jelenséghez, a jelenlegi rezonancia kialakulásának feltételei a következők:
- A teljesítményfrekvencia hasonló az áramkör rezonanciájához.
- A váltakozó áram induktivitásának és kapacitásának vezetőképessége BL = Bc, B = 1 / X.
Gyakorlati alkalmazás
Vegye figyelembe a rezonancia-áramok és feszültségek előnyeit és hátrányait. A rádióadó készülékek által előidézett rezonancia jelenségének legnagyobb előnye. Egyszerű szavakkal: a vevőáramkör tekercset és kondenzátort csatlakoztat az antennához. Az induktivitás megváltoztatásával (például a mag mozgatásával) vagy a kapacitás értékével (például egy légváltozó kondenzátor) beállíthatja a rezonancia frekvenciát. Ennek eredményeként a tekercs feszültsége megemelkedik, és a vevő egy bizonyos rádióhullámot fog elkapni.
Ezek a jelenségek károsak lehetnek az elektrotechnikában, például kábelvezetékeknél. A kábel egy induktancia és kapacitás, amely hosszirányban oszlik meg, ha feszültséget egy hosszú vonalra használnak alapjáratban (amikor a terhelés nincs csatlakoztatva az áramforrással szemben lévő kábel végéhez). Ezért fennáll annak a veszélye, hogy a szigetelés megszakad, ennek elkerülése érdekében egy rakomány előtét csatlakozik.Ugyanígy egy hasonló helyzet az elektronikus alkatrészek, mérőműszerek és más elektromos berendezések meghibásodásához vezethet - ezek a jelenség veszélyes következményei.
következtetés
A feszültségek és áramok rezonanciája érdekes jelenség, amelyet figyelembe kell venni. Csak induktív-kapacitív áramkörökben figyelhető meg. Nagy aktív ellenállású áramkörökben ez nem fordulhat elő. Összefoglalva, röviden megválaszolva a témával kapcsolatos fő kérdéseket:
- Hol és mely láncokban figyelhető meg a rezonancia jelenség?
Induktív kapacitív áramkörökben.
- Milyen feltételek mellett lehet az áramerősség és a feszültség rezonanciája fellépni?
Az egyenlő reakcióképesség mellett fordul elő. Az áramkörnek minimális aktív ellenállással kell rendelkeznie, és az áramellátás frekvenciájának meg kell egyeznie az áramkör rezonancia frekvenciájával.
- Hogyan lehet megtalálni a rezonancia frekvenciát?
Mindkét esetben a képlet szerint:w = (1 / LC) ^ (1/2)
- Hogyan lehet megszüntetni a jelenséget?
Az áramkör ellenállásának növelésével vagy a frekvencia megváltoztatásával.
Most már tudja, hogy mi az áramerősség és a feszültség rezonanciája, mi az előfordulásának feltételei és a gyakorlati alkalmazások. Az anyag összevonása érdekében javasoljuk, hogy nézze meg a hasznos videót a témáról:
Kapcsolódó anyagok: