La ley de la corriente total en palabras simples
El tema familiar para muchos, titulado "Ingeniería eléctrica", contiene en su programa una serie de leyes fundamentales que definen los principios de interacción física para un campo magnético. Extienden su efecto a varios elementos de dispositivos eléctricos, así como a sus estructuras y entornos. La física de los procesos que ocurren en ellos se relaciona con conceptos tan básicos como las corrientes de electricidad y campos. La ley de la corriente total establece una relación entre el movimiento de las cargas eléctricas y el campo magnético creado por ella (más precisamente, su intensidad). La ciencia moderna afirma que su aplicación se extiende a casi todos los entornos.
La esencia de la ley
La ley considerada aplicable en los circuitos magnéticos determina la siguiente relación cuantitativa entre sus componentes constituyentes. La circulación del vector de campo magnético en un circuito cerrado es proporcional a la suma de las corrientes que lo penetran. Para comprender el significado físico de la ley de la corriente total, deberá familiarizarse con la representación gráfica de los procesos descritos por él.
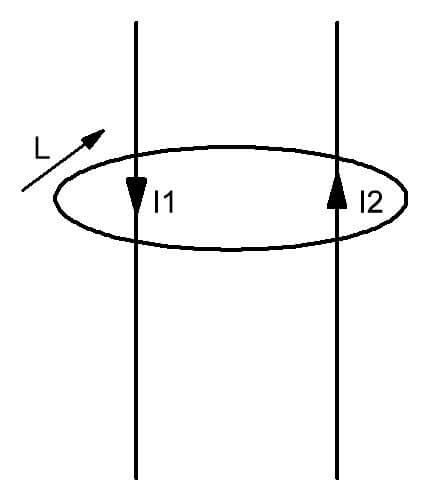
Se puede ver en la figura que alrededor de dos conductores con corrientes I1 e I2 que fluyen a través de ellos, se forma un campo, limitado por el circuito L. Se introduce como una figura cerrada mentalmente imaginada, cuyo plano está perforado por conductores con cargas móviles. En palabras simples, esta ley se puede expresar de la siguiente manera. En presencia de varias corrientes de electricidad a través de la superficie imaginaria imaginaria cubierta por el circuito L, se forma un campo magnético con una distribución dada de tensión dentro de él.
Para la dirección positiva del vector de acuerdo con la ley para el contorno del circuito magnético se selecciona en sentido horario. También es imaginable.
Tal definición del campo de Foucault creado por las corrientes sugiere que la dirección de cada una de las corrientes puede ser arbitraria.
Para referencia! La estructura de campo introducida y el aparato que lo describe deben distinguirse de la circulación del vector electrostático "E", que siempre es igual a cero sin pasar por el circuito. Como resultado de esto, dicho campo se refiere a estructuras potenciales. La circulación del vector "B" del campo magnético nunca es cero. Es por eso que se llama un "vórtice".
Conceptos basicos
De acuerdo con la ley en consideración, el siguiente enfoque simplificado se utiliza para calcular los campos magnéticos. La corriente total se representa como la suma de varios componentes que fluyen a través de una superficie cubierta por un circuito cerrado L. Los cálculos teóricos se pueden representar de la siguiente manera:
- La corriente eléctrica total que fluye a través de los circuitos Σ I es la suma vectorial de I1 e I2.
- En este ejemplo, para determinarlo, use la fórmula:
ΣI = I1 - I2 (menos antes del segundo término significa que las direcciones de las corrientes son opuestas). - Ellos, a su vez, se determinan de acuerdo con la ley conocida en ingeniería eléctrica (regla) gimlet.
El campo magnético a lo largo del contorno se calcula sobre la base de los cálculos obtenidos por técnicas especiales. Para encontrarlo, es necesario integrar este parámetro sobre L usando la ecuación de Maxwell presentada en una de las formas.Se puede aplicar en forma diferencial, pero esto complicará un poco los cálculos.
Enfoque Integrado Simplificado
Si usamos la representación diferencial, será muy difícil expresar la ley de la corriente total en una forma simplificada (en este caso, se deben introducir componentes adicionales). Agregamos a esto que el campo de vórtice magnético creado por las corrientes que se mueven dentro del circuito se determina en este caso teniendo en cuenta la corriente de polarización, que depende de la tasa de cambio de la inducción eléctrica.
Por lo tanto, en la práctica, en TOE, la presentación de fórmulas para corrientes completas en forma de suma de segmentos microscópicamente pequeños de un circuito con campos de Foucault creados en ellos es más popular. Este enfoque implica la aplicación de la ecuación de Maxwell en forma integral. Cuando se implementa, el contorno se divide en pequeños segmentos, que se consideran directos en la primera aproximación (de acuerdo con la ley, se supone que el campo magnético es homogéneo). Este valor, denotado como Um para una sección discreta de longitud ΔL del campo magnético que actúa en el vacío, se define de la siguiente manera:
Um = HL * ΔL
La siguiente fórmula encuentra la tensión total a lo largo del contorno completo L, presentada brevemente en forma integral:
UL = Σ HL * ΔL.
La ley de la corriente total para el vacío.
En su forma final, redactada de acuerdo con todas las reglas de integración, la ley de la corriente total se ve así. La circulación del vector "B" en un circuito cerrado puede representarse como el producto de la constante magnética m en la cantidad de corrientes:
La integral de B sobre dL = la integral de Bl sobre dL = m Σ En
donde n es el número total de conductores con corrientes multidireccionales cubiertas por un circuito mentalmente imaginado L de forma arbitraria.
Cada corriente se tiene en cuenta en esta fórmula tantas veces como esté completamente cubierta por este circuito.
La forma final de los cálculos obtenidos para la ley de la corriente total está muy influenciada por el medio en el que actúa la fuerza (campo) electromagnética inducida.
Impacto ambiental
Las relaciones consideradas para la ley de corrientes y campos que actúan no en el vacío, sino en un medio magnético, toman una forma ligeramente diferente. En este caso, además de los principales componentes de corriente, se introduce el concepto de corrientes microscópicas que surgen en el imán, por ejemplo, o en cualquier material similar al mismo.
La relación necesaria se deriva en su totalidad del teorema sobre la circulación vectorial de la inducción magnética B. En términos simples, se expresa de la siguiente forma. El valor total del vector B cuando se integra sobre el circuito seleccionado es igual a la suma de las macrocorrientes cubiertas por él multiplicadas por el coeficiente de la constante magnética.
Como resultado, la fórmula para "B" en una sustancia está determinada por la expresión:
La integral de B sobre dL = la integral de Bl sobre dL = m(Yo+Yo1)
donde: dL es el elemento discreto del circuito a lo largo de su derivación, Bl es el componente en la dirección de la tangente en un punto arbitrario, bI e I1 son la corriente de conducción y la corriente microscópica (molecular).
Si el campo actúa en un entorno que consiste en materiales arbitrarios, deben tenerse en cuenta las corrientes microscópicas características de estas estructuras.
Estos cálculos también son válidos para el campo creado en el solenoide o en cualquier otro medio con permeabilidad magnética finita.
Para referencia
En el sistema más completo y completo de mediciones de GHS, la intensidad del campo magnético está representada en Oersteds (E). En otro sistema existente (SI), se expresa en amperios por metro (A / metro). Hoy, oersted está siendo reemplazado gradualmente por una unidad más conveniente: amperios por metro.Al traducir los resultados de mediciones o cálculos de SI a GHS, se utiliza la siguiente relación:
1 E = 1000 / (4π) A / m ≈ 79.5775 Amperios / metro.
En la parte final de la revisión, observamos que no importa cuál sea la redacción de la ley de corrientes completas, su esencia permanece sin cambios. En sus propias palabras, esto se puede representar de la siguiente manera: expresa la relación entre las corrientes que penetran en un circuito dado y los campos magnéticos creados en la sustancia.
Finalmente, recomendamos ver un video útil sobre el tema del artículo:
Materiales relacionados: