Primera y segunda leyes de Kirchhoff: una explicación asequible
La primera ley de Kirchhoff.
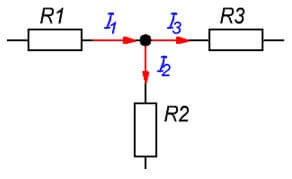
La definición de la primera ley es: "La suma algebraica de las corrientes que fluyen a través de un nodo es cero ". Puedes decir una forma un poco diferente: "Cuántas corrientes fluyeron hacia el nodo, fluyó el mismo número, lo que indica la constancia de la corriente ".
Un nodo de una cadena es un punto de conexión de tres o más ramas. Las corrientes en este caso se distribuyen en proporción a la resistencia de cada rama.
yo1= Yo2+ I3
Esta forma de grabación es válida para circuitos de CC. Si usa la primera ley de Kirchhoff para un circuito de corriente alterna, los valores de voltaje instantáneo se usan con la letra İ y se escriben en forma compleja, y el método de cálculo sigue siendo el mismo:
La forma compleja tiene en cuenta los componentes activos y reactivos.
Segunda ley de Kirchhoff
Si el primero describe la distribución de las corrientes en las ramas, entonces la segunda ley de Kirchhoff es: "La suma de las caídas de voltaje en el circuito es igual a la suma de todos los EMF ".En palabras simples, la redacción dice lo siguiente: "EMF aplicado a una sección de un circuito se distribuirá entre los elementos de este circuito en proporción a las resistencias, es decir, de acuerdo con la ley de Ohm ".
Mientras que para corriente alterna suena así: "La suma de las amplitudes del EMF complejo es igual a la suma de las caídas de voltaje complejas en los elementos ".
Z es la impedancia o resistencia compleja, incluye tanto la parte resistiva como la reactiva (inductancia y capacitancia), que depende de la frecuencia de la corriente alterna (en corriente continua solo hay resistencia activa). A continuación se encuentran las fórmulas de la resistencia compleja del condensador y la inductancia:
Aquí hay una imagen que ilustra lo anterior:
Entonces:
Métodos de cálculo para la primera y segunda leyes de Kirchhoff
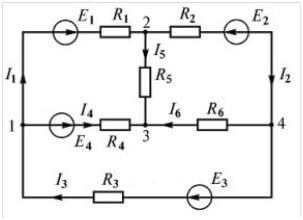
Vamos a poner en práctica el material teórico. Para colocar correctamente los signos en las ecuaciones, debe elegir la dirección del circuito. Echa un vistazo al diagrama:
Sugerimos elegir una dirección en el sentido de las agujas del reloj y marcarla en la figura:
La línea de puntos punteados indica cómo seguir el camino al hacer ecuaciones.
El siguiente paso es componer ecuaciones de acuerdo con las leyes de Kirchhoff. Primero usamos el segundo.Ponemos los signos de esta manera: se coloca un signo menos delante de la fuerza electromotriz si se dirige en sentido antihorario (la dirección que elegimos en el paso anterior), luego, para una fem en sentido horario, ponemos un signo menos. Componemos para cada circuito, teniendo en cuenta los signos.
Para el primero, nos fijamos en la dirección de la EMF, coincide con la línea de puntos y guiones, establezca E1 más E2:
Para el segundo:
Para el tercero:
Los signos de IR (voltaje) dependen de la dirección de las corrientes de bucle. Aquí la regla de signo es la misma que en el caso anterior.
IR se escribe con un signo positivo si la corriente fluye en la dirección de la dirección de derivación del circuito. Y con un signo "-", si la corriente fluye contra la dirección del circuito.
La dirección del recorrido del circuito es una cantidad condicional. Solo se necesita para la disposición de los signos en las ecuaciones, se elige de forma arbitraria y no afecta la exactitud de los cálculos. En algunos casos, una dirección de derivación mal elegida puede complicar el cálculo, pero esto no es crítico.
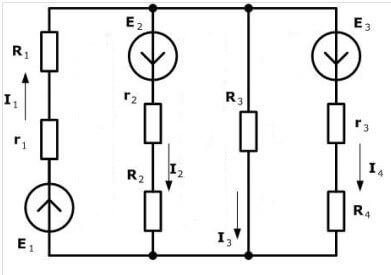
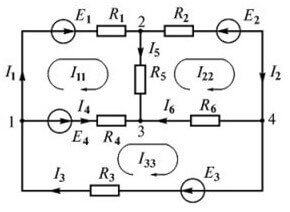
Considere otro circuito:
Hay hasta cuatro fuentes de EMF, pero el procedimiento de cálculo es el mismo, primero elegimos la dirección para hacer las ecuaciones.
Ahora necesitas hacer ecuaciones de acuerdo con la primera ley de Kirchhoff. Para el primer nodo (figura 1 a la izquierda del diagrama):
yo3 fluye y yo1, YO4 se sigue, de ahí los signos. Para el segundo:
Para el tercero:
Pregunta: "Hay cuatro nodos, y solo hay tres ecuaciones, ¿por qué?El hecho es que el número de ecuaciones de la primera regla de Kirchhoff es igual a:
norteecuaciones= nnudos-1
Aquellos. solo hay 1 ecuaciones menos que los nodos, porque esto es suficiente para describir las corrientes en todas las ramas, le aconsejo una vez más que suba al circuito y verifique si todas las corrientes están escritas en las ecuaciones.
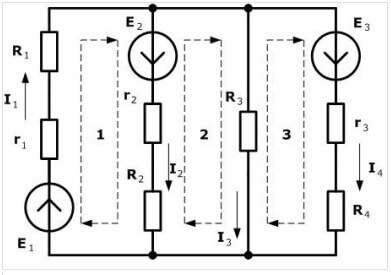
Ahora procedemos a la construcción de ecuaciones por la segunda regla. Para el circuito primario:
Para el segundo circuito:
Para el tercer circuito:
Si sustituimos los valores de tensiones y resistencias reales, resulta que la primera y la segunda ley son justas y se cumplen. Estos son ejemplos simples; en la práctica, se deben resolver problemas mucho más voluminosos.
Conclusión. Lo principal al calcular con la ayuda de la primera y segunda leyes de Kirchhoff es la observancia de la regla para hacer ecuaciones, es decir tenga en cuenta la dirección del flujo de corriente y la derivación del circuito para la disposición correcta de los signos para cada elemento del circuito.
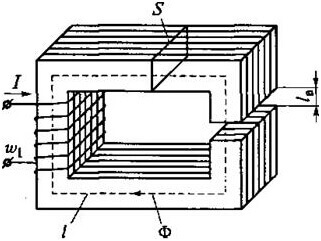
Las leyes de Kirchhoff para el circuito magnético.
Los cálculos de los circuitos magnéticos también son importantes en la ingeniería eléctrica, ambas leyes han encontrado su aplicación aquí. La esencia sigue siendo la misma, pero el tipo y el tamaño cambian, veamos este problema con más detalle. Primero debes lidiar con los conceptos.
La fuerza magnetomotriz (MDS) está determinada por el producto del número de vueltas de la bobina, por la corriente a través de ella:
F = w * i
El voltaje magnético es el producto de la intensidad del campo magnético y la corriente a través de una sección, medida en amperios:
Umetro= H * I
O flujo magnético a través de la resistencia magnética:
Umetro= F * Rmetro
L es la longitud promedio de la gráfica, μr y μ0 - Permeabilidad magnética relativa y absoluta.
Dibujando una analogía, escribimos la primera ley de Kirchhoff para un circuito magnético:
Es decir, la suma de todos los flujos magnéticos a través del nodo es cero. ¿Has notado que suena casi lo mismo que para un circuito eléctrico?
Entonces la segunda ley de Kirchhoff suena como "La suma de los MDS en el circuito magnético es igual a la suma UMETRO (estrés magnético).
El flujo magnético es igual a:
Para un campo magnético alterno:
Depende solo del voltaje a través del devanado, y no de los parámetros del circuito magnético.
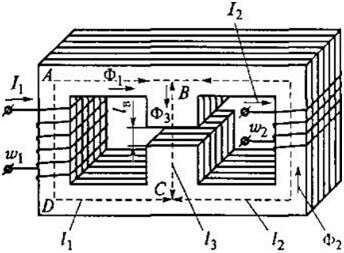
Como ejemplo, considere este contorno:
Luego, para ABCD obtenemos la siguiente fórmula:
Para los circuitos con un entrehierro, las siguientes relaciones son verdaderas:
Resistencia magnética:
Y la resistencia del entrehierro (a la derecha en el núcleo):
Donde S es el área del núcleo.
Para comprender completamente el material y revisar visualmente algunos de los matices del uso de las reglas, le recomendamos que se familiarice con las conferencias que se proporcionan en el video:
Los descubrimientos de Gustav Kirchhoff hicieron una contribución significativa al desarrollo de la ciencia, especialmente la ingeniería eléctrica.Con su ayuda, es bastante simple calcular cualquier circuito eléctrico o magnético, corrientes y voltajes. Esperamos que ahora las reglas de Kirchhoff para circuitos eléctricos y magnéticos sean más claras para usted.
Materiales similares:

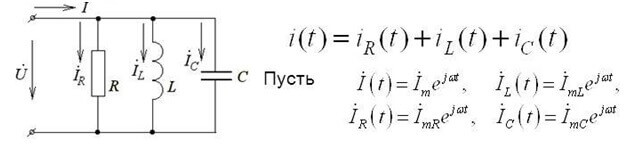
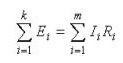
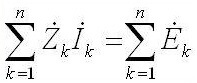
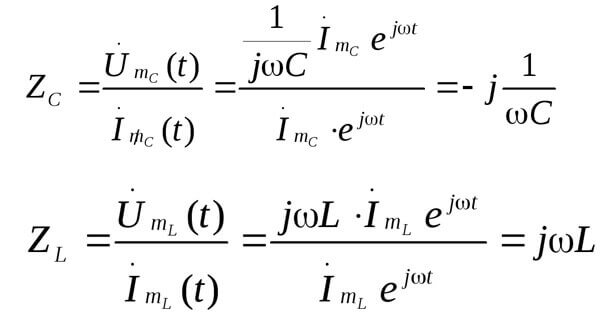

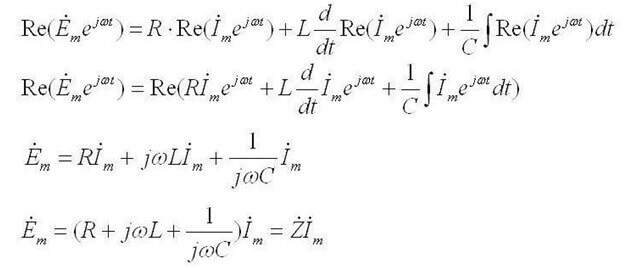
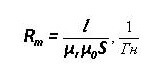
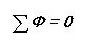
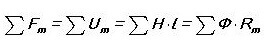
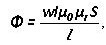
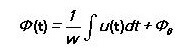
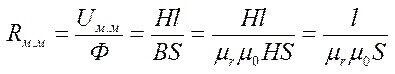
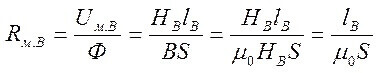


Cuando compongamos su ur de acuerdo con la ley 1 de Kirchhoff, es decir, una buena explicación de la primera ur. ¿Por qué no hay explicación para el segundo y el tercero, cuando todo es mucho más obvio allí? I2 claramente fluye allí, pero por alguna razón tiene un signo positivo
en la tercera ecuación, por lo que generalmente los tres fluyo. ¿Por qué son positivos?
Tenga en cuenta que al comienzo del artículo, la ecuación se considera en la forma I1 = I2 + I3, si transfiere todo al lado izquierdo de la ecuación, I1-I2-I3 = 0. Lo mismo se hizo allí.
Para el segundo nodo:
I1 = I5 + I2
mover todo en una dirección saldrá:
I1-I5-I2 = 0
En comparación con la dirección del bypass del circuito, quedará claro que es mejor cambiar los signos, es decir, multiplicar por menos 1.
Va a salir
-I1 + I5 + I2 = 0
que es equivalente
I2 + I5-I1 = 0