Kirchhoffs erstes und zweites Gesetz - erschwingliche Erklärung
Das erste Gesetz von Kirchhoff
Die Definition des ersten Gesetzes lautet: „Die algebraische Summe der durch einen Knoten fließenden Ströme ist Null. “ Sie können eine etwas andere Form sagen: "Wie viele Ströme in den Knoten flossen, floss dieselbe Anzahl heraus, was die Konstanz des Stroms anzeigt.
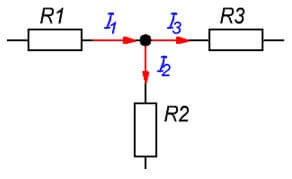
Ein Knoten einer Kette ist ein Verbindungspunkt aus drei oder mehr Zweigen. Die Ströme sind in diesem Fall proportional zum Widerstand jedes Zweigs verteilt.
Ich1= Ich2+ I.3
Diese Form der Aufzeichnung gilt für Gleichstromkreise. Wenn Sie das erste Kirchhoff-Gesetz für einen Wechselstromkreis verwenden, werden Momentanspannungswerte verwendet, mit dem Buchstaben İ bezeichnet und in komplexer Form geschrieben, und die Berechnungsmethode bleibt dieselbe:
Die komplexe Form berücksichtigt sowohl die aktiven als auch die reaktiven Komponenten.
Zweites Gesetz von Kirchhoff
Wenn der erste die Verteilung der Ströme in den Zweigen beschreibt, lautet das zweite Kirchhoff-Gesetz: „Die Summe der Spannungsabfälle im Stromkreis entspricht der Summe aller EMFs. “In einfachen Worten lautet der Wortlaut wie folgt: „Die an einen Abschnitt einer Schaltung angelegte EMF wird proportional zu den Widerständen auf die Elemente dieser Schaltung verteilt, d. H. nach dem Ohmschen Gesetz. "
Während es für Wechselstrom so klingt: "Die Summe der Amplituden der komplexen EMF ist gleich der Summe der komplexen Spannungsabfälle an den Elementen. ".
Z ist die Impedanz oder der komplexe Widerstand, es umfasst sowohl den Widerstandsteil als auch den Blindteil (Induktivität und Kapazität), was von der Frequenz des Wechselstroms abhängt (im Gleichstrom gibt es nur aktiven Widerstand). Nachfolgend sind die Formeln des komplexen Widerstands des Kondensators und der Induktivität aufgeführt:
Hier ist ein Bild, das das Obige veranschaulicht:
Dann:
Berechnungsmethoden für das erste und zweite Gesetz von Kirchhoff
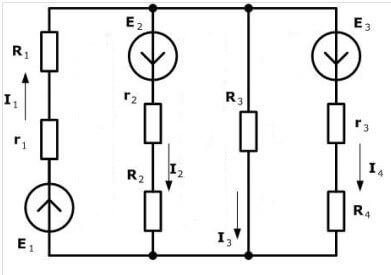
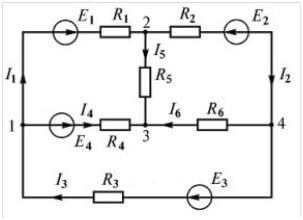
Lassen Sie uns theoretisches Material in die Praxis umsetzen. Um Vorzeichen korrekt in die Gleichungen zu setzen, müssen Sie die Richtung der Schaltung wählen. Schauen Sie sich das Diagramm an:
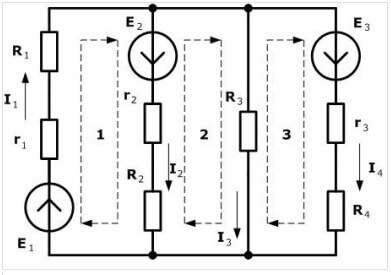
Wir empfehlen, eine Richtung im Uhrzeigersinn zu wählen und diese in der Abbildung zu markieren:
Die gestrichelte Linie zeigt an, wie der Pfad beim Erstellen von Gleichungen verfolgt werden soll.
Der nächste Schritt besteht darin, Gleichungen nach den Gesetzen von Kirchhoff zu erstellen. Erstens benutzen wir den zweiten.Wir setzen die Zeichen so: Ein Minuszeichen wird vor die elektromotorische Kraft gesetzt, wenn sie gegen den Uhrzeigersinn gerichtet ist (die Richtung, die wir im vorherigen Schritt gewählt haben), dann setzen wir für die EMK im Uhrzeigersinn ein Minuszeichen. Wir komponieren für jede Schaltung unter Berücksichtigung der Zeichen.
Zum ersten betrachten wir die Richtung des EMF, die mit der strichpunktierten Linie übereinstimmt, die E1 plus E2 setzt:
Zum zweiten:
Zum dritten:
Die Vorzeichen für IR (Spannung) hängen von der Richtung der Schleifenströme ab. Hier ist die Vorzeichenregel dieselbe wie im vorherigen Fall.
IR wird mit einem positiven Vorzeichen geschrieben, wenn der Strom in Richtung der Schaltungsumgehungsrichtung fließt. Und mit einem "-" - Zeichen, wenn der Strom gegen die Richtung des Stromkreises fließt.
Die Richtung der Stromkreisdurchquerung ist eine bedingte Größe. Es wird nur für die Anordnung von Vorzeichen in Gleichungen benötigt, es wird willkürlich gewählt und hat keinen Einfluss auf die Richtigkeit der Berechnungen. In einigen Fällen kann eine schlecht gewählte Bypassrichtung die Berechnung erschweren, dies ist jedoch nicht kritisch.
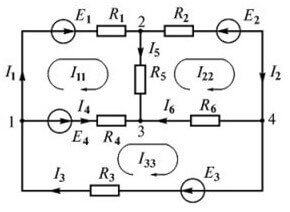
Betrachten Sie eine andere Schaltung:
Es gibt bis zu vier EMF-Quellen, aber das Berechnungsverfahren ist das gleiche. Zuerst wählen wir die Richtung für die Erstellung der Gleichungen.
Jetzt müssen Sie Gleichungen nach dem ersten Gesetz von Kirchhoff machen. Für den ersten Knoten (Abbildung 1 links im Diagramm):
Ich3 fließt ein und ich1Ich4 es folgt, daher die Zeichen. Zum zweiten:
Zum dritten:
Frage: "Es gibt vier Knoten und nur drei Gleichungen. Warum? “Tatsache ist, dass die Anzahl der Gleichungen der ersten Kirchhoff-Regel gleich ist:
N.Gleichungen= nKnoten-1
Das heißt, Es gibt nur 1 weniger Gleichungen als Knoten, weil Dies reicht aus, um die Ströme in allen Zweigen zu beschreiben. Ich rate noch einmal, zum Stromkreis zu gehen und zu prüfen, ob alle Ströme in den Gleichungen geschrieben sind.
Nun fahren wir mit der Konstruktion von Gleichungen nach der zweiten Regel fort. Für den Primärkreis:
Für die zweite Schaltung:
Für die dritte Schaltung:
Wenn wir die Werte der realen Spannungen und Widerstände ersetzen, stellt sich heraus, dass das erste und das zweite Gesetz fair sind und erfüllt werden. Dies sind einfache Beispiele, in der Praxis müssen viel umfangreichere Probleme gelöst werden.
Fazit. Die Hauptsache bei der Berechnung mit Hilfe des ersten und zweiten Kirchhoff-Gesetzes ist die Einhaltung der Regel zur Erstellung von Gleichungen, d.h. Berücksichtigen Sie die Richtung des Stromflusses und den Schaltkreisbypass für die korrekte Anordnung der Vorzeichen für jedes Element des Schaltkreises.
Kirchhoffs Gesetze für den Magnetkreis
Berechnungen von Magnetkreisen sind auch in der Elektrotechnik wichtig, beide Gesetze haben hier ihre Anwendung gefunden. Das Wesentliche bleibt das gleiche, aber der Typ und die Größe ändern sich. Schauen wir uns dieses Problem genauer an. Zuerst müssen Sie sich mit Konzepten befassen.
Die magnetomotorische Kraft (MDS) wird durch das Produkt der Anzahl der Windungen der Spule und durch den Strom durch sie bestimmt:
F = w * i
Die Magnetspannung ist das Produkt aus Magnetfeldstärke und Strom durch einen Abschnitt, gemessen in Ampere:
U.m= H * I.
Oder magnetischer Fluss durch magnetischen Widerstand:
U.m= F * R.m
L ist die durchschnittliche Länge des Diagramms, μr und μ0 - relative und absolute magnetische Permeabilität.
In Analogie schreiben wir das erste Kirchhoff-Gesetz für einen Magnetkreis:
Das heißt, die Summe aller Magnetflüsse durch den Knoten ist Null. Haben Sie bemerkt, dass das fast genauso klingt wie bei einem Stromkreis?
Dann klingt das zweite Gesetz von Kirchhoff wie folgt: „Die Summe der MDS im Magnetkreis ist gleich der Summe U.M. (magnetische Spannung).
Der magnetische Fluss ist gleich:
Für ein magnetisches Wechselfeld:
Dies hängt nur von der Spannung an der Wicklung ab und nicht von den Parametern des Magnetkreises.
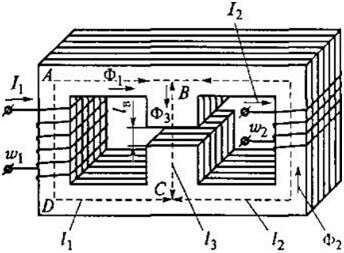
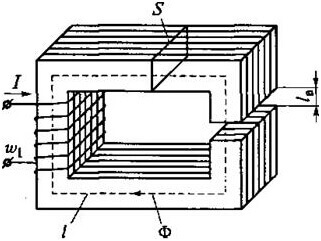
Betrachten Sie als Beispiel diese Kontur:
Dann erhalten wir für ABCD die folgende Formel:
Für Stromkreise mit Luftspalt gelten folgende Zusammenhänge:
Magnetwiderstand:
Und der Widerstand des Luftspalts (rechts am Kern):
Wobei S der Kernbereich ist.
Um das Material vollständig zu verstehen und einige der Nuancen der Verwendung der Regeln visuell zu überprüfen, empfehlen wir Ihnen, sich mit den im Video enthaltenen Vorlesungen vertraut zu machen:
Die Entdeckungen von Gustav Kirchhoff haben einen wesentlichen Beitrag zur Entwicklung der Wissenschaft, insbesondere der Elektrotechnik, geleistet.Mit ihrer Hilfe ist es ganz einfach, elektrische oder magnetische Schaltkreise, Ströme und Spannungen zu berechnen. Wir hoffen, dass Ihnen jetzt Kirchhoffs Regeln für elektrische und magnetische Schaltkreise klarer werden.
Ähnliche Materialien:

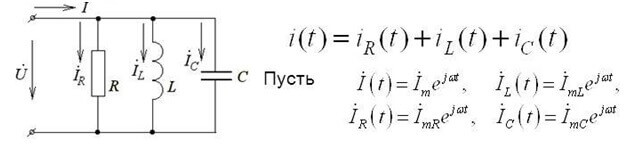
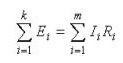
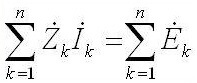
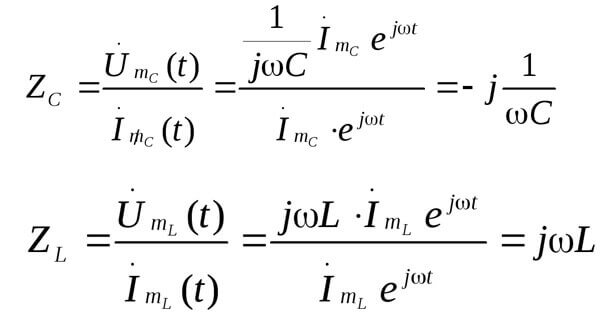

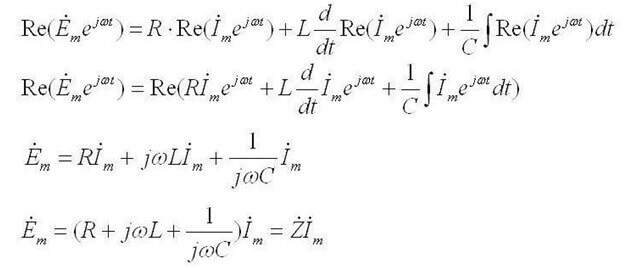
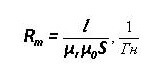
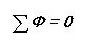
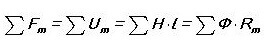
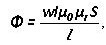
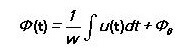
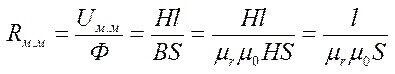
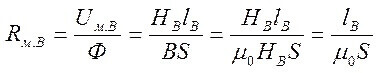


Wenn wir ur nach dem ersten Gesetz von Kirchhoff komponieren, ist das eine gute Erklärung für das erste ur. Warum gibt es keine Erklärung für die zweite und dritte, wenn dort alles viel weniger offensichtlich ist? I2 fließt eindeutig hinein, aber aus irgendeinem Grund hat er ein positives Vorzeichen
in der dritten Gleichung fließen also im Allgemeinen alle drei I ein. Warum sind sie positiv?
Bitte beachten Sie, dass am Anfang des Artikels die Gleichung in der Form I1 = I2 + I3 betrachtet wird. Wenn Sie alles auf die linke Seite der Gleichung übertragen, ist I1-I2-I3 = 0. Das gleiche wurde dort gemacht.
Für den zweiten Knoten:
I1 = I5 + I2
Wenn Sie alles in eine Richtung bewegen, wird Folgendes angezeigt:
I1-I5-I2 = 0
Im Vergleich zur Richtung des Schaltungsbypasses wird deutlich, dass es besser ist, die Vorzeichen zu ändern, dh mit minus 1 zu multiplizieren.
Wird herauskommen
-I1 + I5 + I2 = 0
das ist gleichwertig
I2 + I5-I1 = 0