Kirchhoffovy první a druhé zákony - dostupné vysvětlení
První zákon Kirchhoffa
Definice prvního zákona zní: „Algebraický součet proudů protékajících uzlem je nula. “ Můžete říci trochu jinou formu: "Kolik proudů proudilo do uzlu, vyteklo stejné číslo, což naznačuje stálost proudu. “.
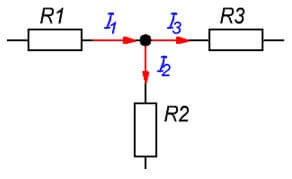
Uzel řetězce je spojovacím bodem tří nebo více větví. Proudy jsou v tomto případě rozděleny úměrně odporu každé větve.
Já1= Já2+ Já3
Tato forma záznamu platí pro stejnosměrné obvody. Pokud použijete první Kirchhoffův zákon pro střídavý proudový obvod, použijí se okamžité hodnoty napětí, jsou označeny písmenem İ a jsou zapsány ve složité formě a metoda výpočtu zůstává stejná:
Složitá forma zohledňuje aktivní i reaktivní složky.
Druhý zákon o Kirchhoffovi
Pokud první popisuje rozdělení proudů ve větvích, pak druhý Kirchhoffův zákon zní: „Součet poklesů napětí v obvodu se rovná součtu všech EMF. “Zjednodušeně řečeno, formulace zní následovně: „EMF aplikovaná na část obvodu bude rozdělena mezi prvky tohoto obvodu v poměru k odporům, tj. podle Ohmova zákona. “
Zatímco pro střídavý proud to zní takto: “Součet amplitud komplexního EMF se rovná součtu poklesů komplexního napětí na prvcích ".
Z je celkový odpor nebo komplexní odpor, zahrnuje jak odporovou část, tak i reaktivní (indukčnost a kapacita), která závisí na frekvenci střídavého proudu (v jednosměrném proudu je pouze aktivní odpor). Níže jsou uvedeny vzorce komplexního odporu kondenzátoru a indukčnosti:
Zde je obrázek ilustrující výše uvedené:
Pak:
Metody výpočtu prvního a druhého zákona Kirchhoffa
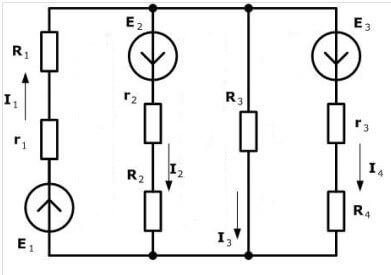
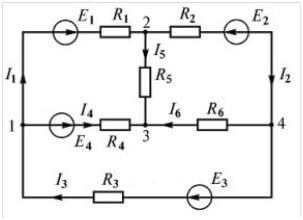
Podívejme se na uvádění teoretických materiálů do praxe. Abyste správně umístili značky do rovnic, musíte zvolit směr obvodu. Podívejte se na diagram:
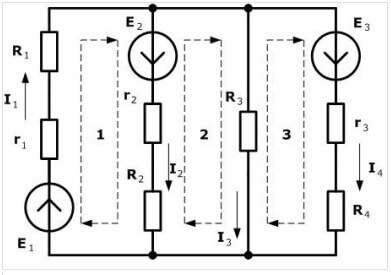
Doporučujeme zvolit směr hodinových ručiček a označit jej na obrázku:
Čárkovaná čára označuje, jak sledovat cestu při vytváření rovnic.
Dalším krokem je sestavení rovnic podle Kirchhoffových zákonů. Nejprve použijeme druhý.Umístili jsme značky takto: znaménko mínus je umístěno před elektromotorickou silou, pokud je namířeno proti směru hodinových ručiček (směr, který jsme vybrali v předchozím kroku), pak pro ručičku ve směru hodinových ručiček dáme znaménko mínus. Skládáme pro každý okruh s přihlédnutím ke značkám.
Nejprve se podíváme na směr EMF, to se shoduje s čárkovanou čarou, set E1 plus E2:
Za druhé:
Za třetí:
Znaky pro IR (napětí) závisí na směru proudů smyčky. Zde je pravidlo znaménka stejné jako v předchozím případě.
IR je zapsáno s kladným znaménkem, pokud proud protéká ve směru obtoku obvodu. A se znaménkem „-“, pokud proud teče proti směru obvodu.
Směr průchodu obvodu je podmíněná veličina. Je potřeba pouze pro uspořádání znamének v rovnicích, je volena libovolně a nemá vliv na správnost výpočtů. V některých případech může výpočet špatně zvolený směr obtoku komplikovat výpočet, ale to není kritické.
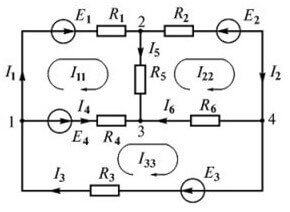
Zvažte další obvod:
Existuje až čtyři zdroje EMF, ale postup výpočtu je stejný, nejdřív si zvolíme směr pro vytváření rovnic.
Nyní musíte udělat rovnice podle prvního zákona Kirchhoffa. Pro první uzel (obrázek 1 vlevo od diagramu):
Já3 proudí dovnitř a já1, Já4 z toho vyplývá znamení. Za druhé:
Za třetí:
Otázka: "Existují čtyři uzly a existují pouze tři rovnice, proč? “Faktem je, že počet rovnic prvního Kirchhoffova pravidla se rovná:
Nrovnice= nuzlů-1
I.e. existuje pouze o 1 méně rovnic než uzlů, protože to stačí k popisu proudů ve všech větvích, radím znovu jít do obvodu a zkontrolovat, zda jsou všechny proudy zapsány do rovnic.
Nyní přistupujeme ke konstrukci rovnic podle druhého pravidla. Pro primární obvod:
Pro druhý okruh:
Pro třetí okruh:
Pokud nahradíme hodnoty skutečných napětí a odporů, ukáže se, že první a druhý zákon jsou spravedlivé a jsou splněny. Toto jsou jednoduché příklady: v praxi je třeba vyřešit mnohem objemnější problémy.
Závěr. Hlavní věcí při výpočtu pomocí prvního a druhého Kirchhoffova zákona je dodržování pravidla pro vytváření rovnic, tzn. vzít v úvahu směr proudu proudu a obtoku obvodu pro správné uspořádání značek pro každý prvek obvodu.
Kirchhoffovy zákony pro magnetický obvod
Výpočty magnetických obvodů jsou také důležité v elektrotechnice, oba zákony zde našly své uplatnění. Podstata zůstává stejná, ale mění se typ a velikost, pojďme se na tento problém podívat podrobněji. Nejprve se musíte vypořádat s pojmy.
Magnetomotorická síla (MDS) je určena součinem počtu závitů cívky, proudem skrz ni:
F = w * i
Magnetické napětí je součin síly a proudu magnetického pole průřezem, měřeno v ampérech:
Um= H * I
Nebo magnetický tok prostřednictvím magnetického odporu:
Um= F * Rm
L je průměrná délka grafu, μr a μ0 - relativní a absolutní magnetická propustnost.
Na základě analogie píšeme první Kirchhoffův zákon pro magnetický obvod:
To znamená, že součet všech magnetických toků v uzlu je nulový. Všimli jste si, že to zní téměř stejně jako u elektrického obvodu?
Pak druhý zákon Kirchhoffa zní jako „Součet MDS v magnetickém obvodu je roven součtu UM (magnetické napětí).
Magnetický tok se rovná:
Pro střídavé magnetické pole:
Závisí to pouze na napětí přes vinutí a ne na parametrech magnetického obvodu.
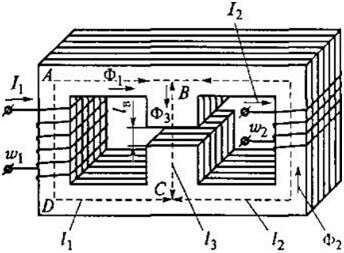
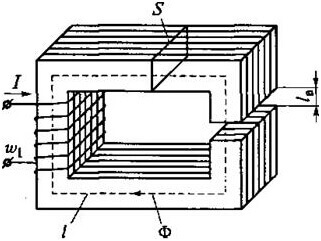
Jako příklad zvažte tento obrys:
Pak pro ABCD dostaneme následující vzorec:
U obvodů se vzduchovou mezerou platí následující vztahy:
Magnetická odolnost:
A odpor vzduchové mezery (vpravo na jádru):
Kde S je hlavní oblast.
Chcete-li plně porozumět materiálu a vizuálně zkontrolovat některé nuance používání pravidel, doporučujeme vám seznámit se s přednáškami, které jsou na videu uvedeny:
Objevy Gustava Kirchhoffa významně přispěly k rozvoji vědy, zejména elektrotechniky.S jejich pomocí je poměrně jednoduché spočítat jakýkoli elektrický nebo magnetický obvod, proudy v něm a napětí. Doufáme, že Kirchhoffova pravidla pro elektrické a magnetické obvody jsou pro vás nyní jasnější.
Podobné materiály:

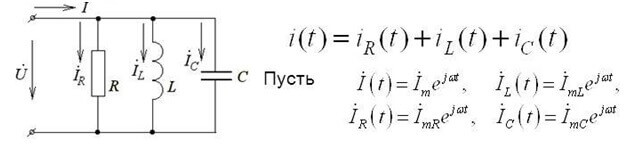
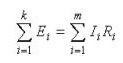
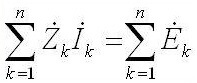
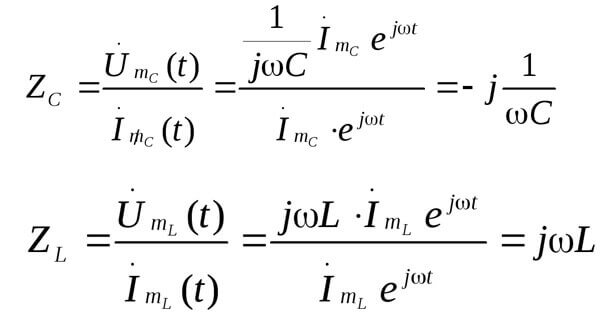

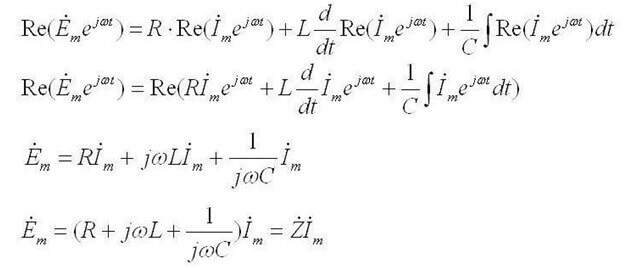
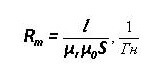
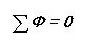
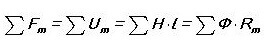
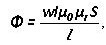
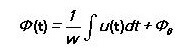
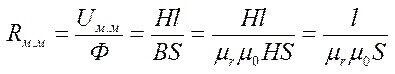
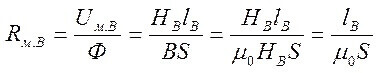


Když skládáme ur podle prvního zákona Kirchhoffa, je to dobré vysvětlení prvního ur. Proč neexistuje vysvětlení pro druhé a třetí, když je zde vše mnohem více nevhodné? I2 tam jasně proudí, ale z nějakého důvodu má pozitivní znamení
ve třetí rovnici, takže obecně všechny tři, do kterých proudím. Proč jsou pozitivní?
Vezměte prosím na vědomí, že na začátku článku se rovnice považuje za formu I1 = I2 + I3, pokud přenesete vše na levou stranu rovnice, I1-I2-I3 = 0. Totéž se stalo.
Pro druhý uzel:
I1 = I5 + I2
vyjde vše v jednom směru:
I1-I5-I2 = 0
Ve srovnání se směrem obtoku obvodu je zřejmé, že je lepší změnit znaménka, to znamená násobit mínus 1.
Vyjde
-I1 + I5 + I2 = 0
což je ekvivalentní
I2 + I5-I1 = 0