قانون التيار الكلي بكلمات بسيطة

يحتوي موضوع مألوف يسمى الهندسة الكهربائية في برنامجها على سلسلة من القوانين الأساسية التي تحدد مبادئ التفاعل الفيزيائي للمجال المغناطيسي. يمتد تأثيرها إلى عناصر مختلفة من الأجهزة الكهربائية ، وكذلك هياكلها وبيئاتها. تتعلق فيزياء العمليات التي تحدث فيها بمفاهيم أساسية مثل تيارات الكهرباء والمجالات. يحدد قانون التيار الإجمالي العلاقة بين حركة الشحنات الكهربائية والمجال المغناطيسي الذي أنشأه (بتعبير أدق ، شدته). يدعي العلم الحديث أن تطبيقه يمتد إلى جميع البيئات تقريبًا.

جوهر القانون

يحدد القانون المدروس المطبق في الدوائر المغناطيسية العلاقة الكمية التالية بين مكوناته. يتناسب دوران ناقل المجال المغناطيسي في حلقة مغلقة مع مجموع التيارات التي تخترقه. لفهم المعنى المادي لقانون التيار الكلي ، ستحتاج إلى التعرف على التمثيل البياني للعمليات التي وصفها.

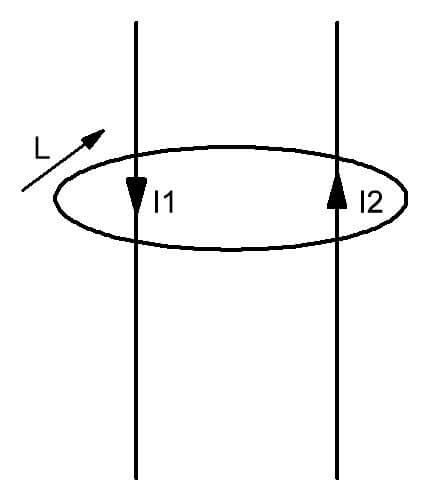
يمكن أن نرى من الشكل أن حوالي اثنين من الموصلات التي تتدفق من خلالها تيارات I1 و I2 ، يتم تشكيل مجال محدود بواسطة الدائرة L. ويتم تقديمه كشكل مغلق متخيل عقليًا ، حيث يتم اختراق مستوى الموصلات بواسطة شحنات متحركة. بكلمات بسيطة ، يمكن التعبير عن هذا القانون على النحو التالي. في وجود عدة تدفقات للكهرباء من خلال السطح التخيلي المغطى بالكفاف L ، يتشكل داخله مجال مغناطيسي بتوزيع شدة محدد مسبقًا.

يتم تحديد الاتجاه الإيجابي للمتجه وفقًا لقانون تحديد محيط الدائرة المغناطيسية في اتجاه عقارب الساعة. كما يمكن تخيله.

يشير هذا التعريف لحقل الدوامة الذي أنشأته التيارات إلى أن اتجاه كل تيارات يمكن أن يكون تعسفيًا.

كمرجع! يجب تمييز بنية المجال المدخلة والجهاز الذي يصفها عن دوران ناقلات الكهرباء الساكنة "E" ، والتي تساوي دائمًا صفر تجاوز الدائرة. ونتيجة لذلك ، يشير هذا المجال إلى الهياكل المحتملة. لا يكون دوران المتجه "B" للمجال المغناطيسي صفرًا. هذا هو السبب في أنها تسمى "دوامة".

مفاهيم أساسية

وفقًا للقانون قيد النظر ، يتم استخدام النهج المبسط التالي لحساب المجالات المغناطيسية. يتم تمثيل التيار الإجمالي كمجموع عدة مكونات تتدفق عبر سطح مغطى بدائرة مغلقة L. يمكن تمثيل الحسابات النظرية على النحو التالي:

1. إجمالي التيار الكهربائي المتدفق عبر الدوائر Σ I هو مجموع المتجه لـ I1 و I2.
2. في هذا المثال ، لتحديد ذلك ، استخدم الصيغة:
   ΣI = I1 - I2 (ناقص قبل الحد الثاني يعني أن اتجاهات التيارات متقابلة).
3. يتم تحديدها بدورها وفقًا للقانون المعروف في الهندسة الكهربائية (القاعدة) مخرز.

يتم حساب المجال المغناطيسي على طول الكفاف على أساس الحسابات التي تم الحصول عليها بتقنيات خاصة. للعثور عليه ، من الضروري دمج هذه المعلمة على L باستخدام معادلة Maxwell المقدمة في أحد الأشكال.يمكن تطبيقه في شكل تفاضلي ، ولكن هذا سيعقد الحسابات إلى حد ما.

نهج متكامل مبسط

إذا استخدمنا التمثيل التفاضلي ، فسيكون من الصعب جدًا التعبير عن قانون التيار الإجمالي بشكل مبسط (في هذه الحالة ، يجب إدخال مكونات إضافية فيه). نضيف إلى ذلك أن مجال الدوامة المغناطيسية الناتج عن التيارات المتحركة داخل الدائرة يتم تحديده في هذه الحالة مع الأخذ بعين الاعتبار تيار التحيز ، والذي يعتمد على معدل تغير الحث الكهربائي.

لذلك ، في الممارسة العملية ، في TOE ، فإن عرض الصيغ للتيارات الكاملة في شكل تجميع لأجزاء صغيرة مجهرية من دائرة تحتوي على حقول دوامة تم إنشاؤها فيها أكثر شيوعًا. يتضمن هذا النهج تطبيق معادلة ماكسويل بشكل متكامل. عندما يتم تنفيذه ، ينقسم الكفاف إلى أجزاء صغيرة ، والتي تعتبر مباشرة في التقريب الأول (وفقًا للقانون يفترض أن المجال المغناطيسي متجانس). يتم تعريف هذه القيمة ، التي يشار إليها باسم Um لقسم منفصل واحد بطول ميكرولتر من المجال المغناطيسي الذي يعمل في الفراغ ، على النحو التالي:

أم = HL * ΔL

تم العثور على التوتر الكلي على طول الكفاف الكامل L ، المقدم لفترة وجيزة في شكل متكامل ، بالصيغة التالية:

UL = Σ HL * ΔL.

قانون التيار الكلي للفراغ

في شكله النهائي ، تم وضعه وفقًا لجميع قواعد التكامل ، يبدو قانون إجمالي التيار هكذا. يمكن تمثيل دوران المتجه "B" في حلقة مغلقة كمنتج للثابت المغناطيسي م في كمية التيارات:

تكامل B عبر dL = تكامل Bl عبر dL = م Σ في

حيث n هو العدد الإجمالي للموصلات ذات التيارات متعددة الاتجاهات التي تغطيها دائرة متخيلة ذهنيًا L ذات شكل اعتباطي.

يتم أخذ كل تيار في الاعتبار في هذه الصيغة عدة مرات حيث يتم تغطيته بالكامل بواسطة هذه الدائرة.

يتأثر الشكل النهائي للحسابات التي تم الحصول عليها لقانون التيار الكلي بشكل كبير بالوسط الذي تعمل فيه القوة الكهرومغناطيسية المستحثة (المجال).

تأثير بيئي

إن العلاقات المدروسة لقانون التيارات والمجالات التي لا تعمل في فراغ ، ولكن في وسط مغناطيسي ، تأخذ شكلًا مختلفًا قليلاً. في هذه الحالة ، بالإضافة إلى المكونات الحالية الرئيسية ، تم إدخال مفهوم التيارات المجهرية الناشئة في المغناطيس ، على سبيل المثال ، أو في أي مادة مماثلة له.

يتم اشتقاق العلاقة الكاملة بالكامل من نظرية حول الدوران المتجه للحث المغناطيسي B. بعبارات بسيطة ، يتم التعبير عنها في الشكل التالي. القيمة الإجمالية للمتجه B عند دمجه في الدائرة المختارة تساوي مجموع التيارات الكلية التي يغطيها مضروبة في معامل الثابت المغناطيسي.

ونتيجة لذلك ، يتم تحديد صيغة "B" في مادة ما بواسطة التعبير:

تكامل B عبر dL = تكامل Bl عبر dL = م(أنا+أنا1)

حيث: dL هو العنصر المنفصل للدائرة على طول الالتفاف ، Bl هو المكون في اتجاه المماس عند نقطة عشوائية ، bI و I1 هما تيار التوصيل والتيار المجهري (الجزيئي).

إذا كان المجال يعمل في بيئة تتكون من مواد تعسفية ، فيجب أن تؤخذ في الاعتبار التيارات المجهرية المميزة لهذه الهياكل.

هذه الحسابات صحيحة أيضًا للحقل الذي تم إنشاؤه في الملف اللولبي أو في أي وسيط آخر ذو نفاذية مغناطيسية محدودة.

كمرجع

في النظام الأكثر اكتمالا وشمولا لقياسات GHS ، يتم تمثيل شدة المجال المغناطيسي في Oersteds (E). في نظام آخر موجود (SI) ، يتم التعبير عنه بالأمبير لكل متر (A / متر). اليوم ، يتم استبدال oersted تدريجياً بوحدة تشغيل أكثر ملاءمة - أمبير لكل متر.عند ترجمة نتائج القياسات أو الحسابات من SI إلى GHS ، يتم استخدام النسبة التالية:

1 e = 1000 / (4π) A / m ≈ 79.5775 أمبير / متر.

في الجزء الأخير من المراجعة ، نلاحظ أنه بغض النظر عن صيغة قانون التيارات الكاملة المستخدمة ، فإن جوهرها يبقى دون تغيير. في كلماته الخاصة ، يمكن تمثيل ذلك على النحو التالي: فهو يعبر عن العلاقة بين التيارات التي تخترق هذه الدائرة والمجالات المغناطيسية التي تم إنشاؤها في المادة.

أخيرًا ، نوصي بمشاهدة فيديو مفيد حول موضوع المقال:

مواد ذات صلة:

• ما هو المجال الكهربائي
• مقاومة الموصل مقابل درجة الحرارة
• أعظم اكتشافات نيكولا تيسلا