قانونا Kirchhoff الأول والثاني - شرح بأسعار معقولة
القانون الأول ل Kirchhoff
تعريف القانون الأول هو:مجموع الجبر للتيارات المتدفقة عبر العقدة هو صفر. " يمكنك قول شكل مختلف قليلاً: "كم عدد التيارات المتدفقة في العقدة ، نفس العدد يتدفق ، مما يشير إلى ثبات التيار ".
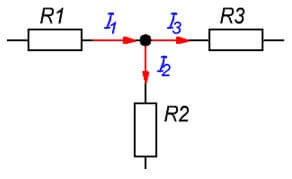
عقدة السلسلة هي نقطة اتصال لثلاثة فروع أو أكثر. يتم توزيع التيارات في هذه الحالة بما يتناسب مع مقاومة كل فرع.
أنا1= أنا2+ أنا3
هذا النوع من التسجيل صالح لدوائر التيار المستمر. إذا كنت تستخدم قانون Kirchhoff الأول لدائرة تيار متناوب ، فسيتم استخدام قيم الجهد اللحظي ، ويُشار إليها بالحرف İ ويتم كتابتها في شكل معقد ، وتظل طريقة الحساب كما هي:
يأخذ الشكل المعقد في الاعتبار كل من المكونات النشطة والتفاعلية.
القانون الثاني ل Kirchhoff
إذا كان الأول يصف توزيع التيارات في الفروع ، فإن قانون كيرشوف الثاني هو:مجموع قطرات الجهد في الدائرة يساوي مجموع جميع المجالات الكهرومغناطيسية. "بعبارات بسيطة ، تنص الصياغة على ما يلي: "سيتم توزيع المجالات الكهرومغناطيسية المطبقة على قسم من الدائرة على عناصر هذه الدائرة بما يتناسب مع المقاومات ، أي وفقًا لقانون أوم ".
في حين أن التيار المتناوب يبدو كالتالي: "مجموع اتساعات EMF المعقد يساوي مجموع قطرات الجهد المعقد على العناصر ".
Z هي المقاومة أو المقاومة المعقدة ، وهي تشمل كلاً من الجزء المقاوم والجزء التفاعلي (الحث والسعة) ، والذي يعتمد على تردد التيار المتناوب (في التيار المباشر لا توجد سوى مقاومة نشطة). فيما يلي صيغ المقاومة المعقدة للمكثف والمحث:
هنا صورة توضح ما سبق:
ثم:
طرق الحساب للقوانين الأولى والثانية من Kirchhoff
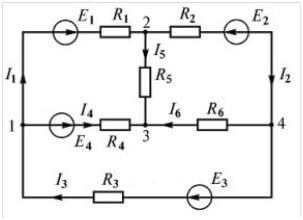
دعونا نضع المادة النظرية موضع التنفيذ. لوضع العلامات بشكل صحيح في المعادلات ، تحتاج إلى اختيار اتجاه الدائرة. نلقي نظرة على الرسم التخطيطي:
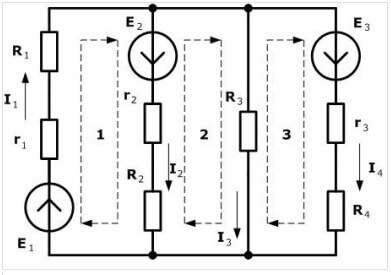
نقترح اختيار اتجاه في اتجاه عقارب الساعة ووضع علامة عليه في الشكل:
يشير الخط المتقطع إلى كيفية اتباع المسار عند عمل المعادلات.
الخطوة التالية هي تكوين المعادلات وفقًا لقوانين Kirchhoff. أولا نستخدم الثاني.نضع العلامات على النحو التالي: يتم وضع علامة ناقص أمام قوة الحركة الكهربائية إذا تم توجيهها عكس اتجاه عقارب الساعة (الاتجاه الذي اخترناه في الخطوة السابقة) ، ثم نضع علامة ناقص في اتجاه عقارب الساعة. نقوم بتأليف كل دائرة ، مع مراعاة العلامات.
أولاً ، ننظر إلى اتجاه EMF ، وهو يتزامن مع الخط المنقط ، وتعيين E1 بالإضافة إلى E2:
للمرة الثانية:
عن الثالث:
تعتمد علامات IR (الجهد) على اتجاه تيارات الحلقة. هنا قاعدة التوقيع هي نفسها كما في الحالة السابقة.
يتم كتابة IR بعلامة موجبة إذا كان التيار يتدفق في اتجاه اتجاه تجاوز الدائرة. ومع وجود علامة "-" ، إذا كان التيار يتدفق مقابل اتجاه الدائرة.
اتجاه اجتياز الدارة هو كمية مشروطة. هو مطلوب فقط لترتيب العلامات في المعادلات ، ويتم اختياره بشكل تعسفي ولا يؤثر على صحة الحسابات. في بعض الحالات ، يمكن أن يؤدي اتجاه الالتفاف الذي تم اختياره بشكل سيئ إلى تعقيد الحساب ، ولكن هذا ليس بالغ الأهمية.
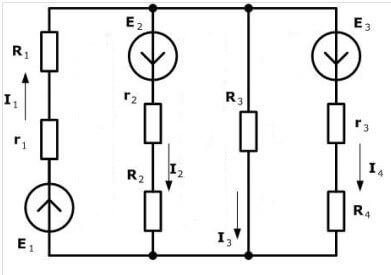
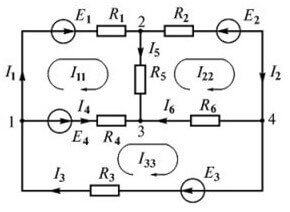
النظر في دائرة أخرى:
هناك ما يصل إلى أربعة مصادر للمجالات الكهرومغناطيسية ، ولكن إجراء الحساب هو نفسه ، أولاً نختار الاتجاه لإجراء المعادلات.
تحتاج الآن إلى إجراء معادلات وفقًا للقانون الأول لـ Kirchhoff. للعقدة الأولى (الشكل 1 على يسار الرسم البياني):
أنا3 يتدفق ، وأنا1أنا4 يتبع ذلك ، ومن هنا العلامات. للمرة الثانية:
عن الثالث:
السؤال: "هناك أربع عقد ، وثلاث معادلات فقط ، لماذا؟ "الحقيقة هي أن عدد معادلات قاعدة Kirchhoff الأولى تساوي:
نالمعادلات= نعقدة-1
على سبيل المثال هناك معادلات أقل من العقد فقط ، لأنه هذا يكفي لوصف التيارات في جميع الفروع ، أنصحك مرة أخرى بالذهاب إلى الدائرة والتحقق مما إذا كانت جميع التيارات مكتوبة في المعادلات.
الآن ننتقل إلى بناء المعادلات بالقاعدة الثانية. للدائرة الابتدائية:
للدائرة الثانية:
للدائرة الثالثة:
إذا استبدلنا قيم الفولتية والمقاومة الحقيقية ، فقد اتضح أن القانونين الأول والثاني عادلان ويتم الوفاء به. هذه أمثلة بسيطة ؛ في الممارسة العملية ، يجب حل مشاكل أكثر ضخامة.
الخلاصة. الشيء الرئيسي عند الحساب بمساعدة قوانين Kirchhoff الأولى والثانية هو مراعاة قاعدة صنع المعادلات ، أي تأخذ في الاعتبار اتجاه التدفق الحالي وتجاوز الدائرة للترتيب الصحيح للعلامات لكل عنصر من عناصر الدائرة.
قوانين كيرشوف للدائرة المغناطيسية
حسابات الدوائر المغناطيسية مهمة أيضًا في الهندسة الكهربائية ، وقد وجد كلا القانونين تطبيقهما هنا. يبقى الجوهر هو نفسه ، ولكن النوع والحجم يتغيران ، دعنا ننظر إلى هذه المشكلة بمزيد من التفصيل. تحتاج أولاً إلى التعامل مع المفاهيم.
يتم تحديد قوة الحركة المغناطيسية (MDS) من خلال منتج عدد لفات الملف ، من خلال التيار من خلاله:
F = w * i
الجهد المغناطيسي هو نتاج قوة المجال المغناطيسي والتيار من خلال قسم ، يقاس أمبير:
شم= H * I
أو التدفق المغناطيسي من خلال المقاومة المغناطيسية:
شم= F * Rم
L هو متوسط طول المؤامرة ، μص و μ0 - النفاذية المغناطيسية النسبية والمطلقة.
برسم القياس ، نكتب أول قانون Kirchhoff للدائرة المغناطيسية:
أي أن مجموع كل التدفقات المغناطيسية عبر العقدة هو صفر. هل لاحظت أن الأصوات تبدو متشابهة تمامًا مثل الدائرة الكهربائية؟
ثم يبدو القانون الثاني لـ Kirchhoff مثل "مجموع MDS في الدائرة المغناطيسية يساوي المجموع Uم (الإجهاد المغناطيسي).
التدفق المغناطيسي يساوي:
بالنسبة للمجال المغناطيسي المتناوب:
يعتمد فقط على الجهد عبر اللف ، وليس على معلمات الدائرة المغناطيسية.
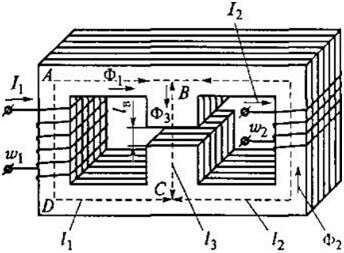
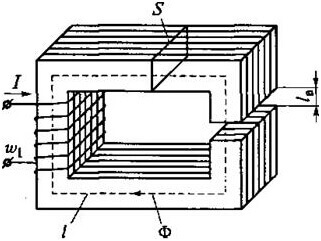
كمثال ، خذ بعين الاعتبار هذا الكفاف:
ثم نحصل على ABCD الصيغة التالية:
بالنسبة للدوائر التي بها فجوة هوائية ، تكون العلاقات التالية صحيحة:
المقاومة المغناطيسية:
ومقاومة الفجوة الهوائية (على اليمين على القلب):
حيث S هي المنطقة الأساسية.
لفهم المادة بشكل كامل ومراجعة بعض الفروق الدقيقة في استخدام القواعد بشكل مرئي ، نوصي بأن تتعرف على المحاضرات المقدمة في الفيديو:
ساهمت اكتشافات غوستاف كيرشوف بشكل كبير في تطوير العلوم ، وخاصة الهندسة الكهربائية.بمساعدتهم ، من السهل جدًا حساب أي دائرة كهربائية أو مغناطيسية وتيارات فيها وفولتية. نأمل أن تصبح قواعد Kirchhoff للدوائر الكهربائية والمغناطيسية أكثر وضوحًا بالنسبة لك.
مواد مماثلة:

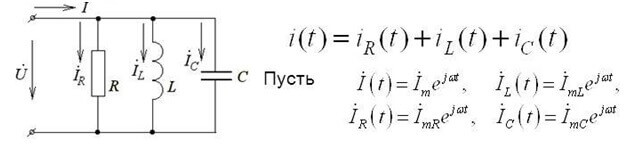
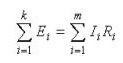
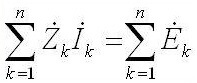
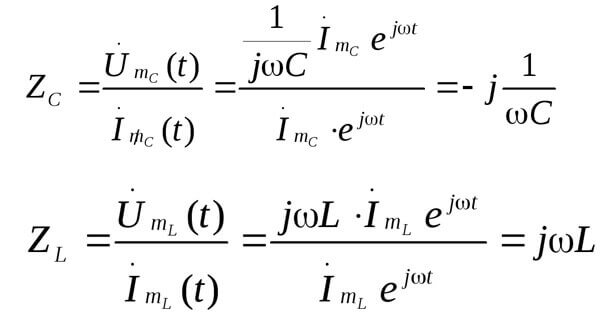

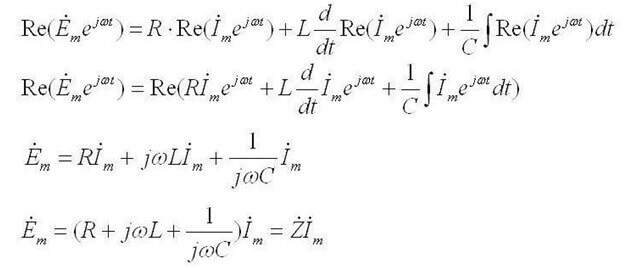
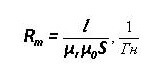
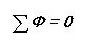
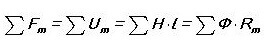
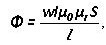
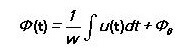
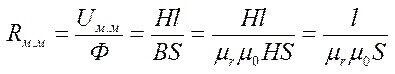
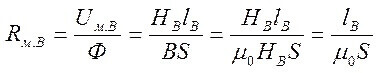


عندما نقوم بتأليف ur الخاص بك وفقًا للقانون الأول لـ Kirchhoff ، وهذا هو ، تفسير جيد لأول ur. لماذا لا يوجد تفسير للثاني والثالث ، عندما يكون كل شيء أكثر وضوحًا هناك؟ يتدفق I2 بوضوح هناك ، ولكن لسبب ما لديه علامة إيجابية
في المعادلة الثالثة ، لذلك بشكل عام ، أتدفق إلى الثلاثة. لماذا هم إيجابيون؟
يرجى ملاحظة أنه في بداية المقال ، يتم اعتبار المعادلة بالشكل I1 = I2 + I3 ، إذا قمت بنقل كل شيء إلى الجانب الأيسر من المعادلة ، I1-I2-I3 = 0. نفس الشيء تم القيام به هناك.
للعقدة الثانية:
I1 = I5 + I2
تحريك كل شيء في اتجاه واحد سيخرج:
I1-I5-I2 = 0
مقارنة مع اتجاه تجاوز الدائرة ، يصبح من الواضح أنه من الأفضل تغيير العلامات ، أي الضرب في ناقص 1.
سيخرج
-I1 + I5 + I2 = 0
وهو ما يعادل
I2 + I5-I1 = 0