Lagen om totalström i enkla ord
Det ämne som är känt för många, med titeln "Elektroteknik", innehåller i sitt program en serie grundläggande lagar som definierar principerna för fysisk interaktion för ett magnetfält. De utvidgar sin effekt till olika element i elektriska apparater, liksom deras strukturer och miljöer. Fysiken i de processer som förekommer i dem gäller sådana grundläggande begrepp som strömmar av elektricitet och fält. Lagen om total ström skapar ett förhållande mellan rörelsen av elektriska laddningar och det magnetfält som skapas av den (mer exakt, dess intensitet). Modern vetenskap hävdar att dess tillämpning sträcker sig till nästan alla miljöer.
Kärnan i lagen
Den aktuella lagen, som är tillämplig i magnetkretsar, bestämmer följande kvantitativa förhållande mellan dess beståndsdelar. Cirkulationen av magnetfältvektorn i en sluten slinga är proportionell mot summan av strömmarna som tränger igenom den. För att förstå den fysiska betydelsen av lagen om total ström måste du bekanta dig med den grafiska framställningen av de processer som beskrivs av honom.
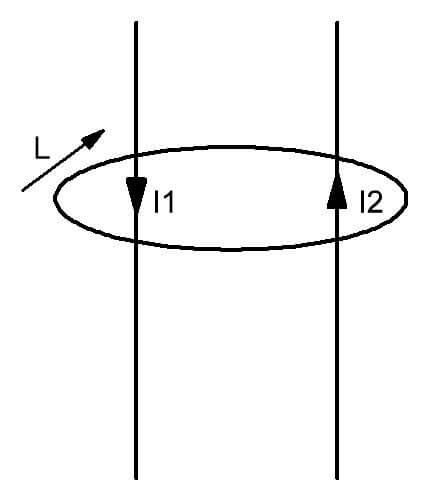
Det framgår av figuren att ungefär två ledare med strömmar I1 och I2 som strömmar genom dem, ett fält bildas begränsat av kretsen L. Det införs som en mentalt föreställd stängd figur, vars plan är genomborrad av ledare med rörliga laddningar. Med enkla ord kan denna lag uttryckas på följande sätt. I närvaro av flera strömmar av elektricitet genom den imaginära imaginära ytan som täcks av kretsen L, bildas ett magnetfält med en given spänningsfördelning i den.
För vektorns positiva riktning i enlighet med lagen för magnetkretsens kontur väljs medurs. Det är också tänkbart.
En sådan definition av virvelfältet skapat av strömmarna antyder att riktningen för var och en av strömmarna kan vara godtycklig.
Som referens! Den införda fältstrukturen och apparaten som beskriver den bör skiljas från cirkulationen av den elektrostatiska vektorn "E", som alltid är lika med noll som förbigår kretsen. Som ett resultat av detta avser ett sådant fält potentiella strukturer. Cirkulationen av vektorn "B" i magnetfältet är aldrig noll. Det är därför det kallas en "virvel".
Grundläggande koncept
I enlighet med den aktuella lagen används följande förenklade metod för att beräkna magnetfält. Den totala strömmen representeras som summan av flera komponenter som strömmar genom en yta täckt av en sluten krets L. Teoretiska beräkningar kan representeras enligt följande:
- Det totala elektriska flödet som tränger igenom kretsarna Σ I är vektorn summan av I1 och I2.
- För att bestämma det i detta exempel använder du formeln:
ΣI = I1 - I2 (minus före den andra termen betyder att de aktuella riktningarna är motsatta). - De bestäms i sin tur enligt lagen känd inom elektroteknik (regel) gimlet.
Magnetfältet längs konturen beräknas på grundval av beräkningarna erhållna med specialtekniker. För att hitta det är det nödvändigt att integrera denna parameter över L med hjälp av Maxwell-ekvationen som presenteras i en av formulärerna.Det kan tillämpas i differentiell form, men det kommer att komplicera beräkningarna något.
Förenklad integrerad strategi
Om vi använder den differentiella representationen kommer det att vara mycket svårt att uttrycka den totala gällande lagen i en förenklad form (i detta fall måste ytterligare komponenter införas i den). Vi lägger till detta att det magnetiska virvelfältet som skapas av strömmarna som rör sig inom kretsen bestäms i detta fall med hänsyn till förspänningsströmmen, som beror på hastigheten för förändring av elektrisk induktion.
Därför är i praktiken, i TOE, presentation av formler för fullströmmar i form av summering av mikroskopiskt små segment av en krets med virvelfält skapade i dem mer populär. Denna metod involverar tillämpningen av Maxwell-ekvationen i integrerad form. När den implementeras är konturen uppdelad i små segment, som anses vara raka i den första tillnärmningen (enligt lagen antas det att magnetfältet är enhetligt). Detta värde, betecknat Um för en diskret del av längden ΔL på magnetfältet som verkar i vakuum, definieras enligt följande:
Um = HL * ΔL
Den totala spänningen längs hela konturen L, kort presenterad i integrerad form, hittas med följande formel:
UL = Σ HL * ΔL.
Lagen om den totala strömmen för vakuum
I sin slutliga form, upprättad enligt alla integrationsregler, ser lagen om total ström ut så här. Cirkulation av vektorn "B" i en sluten slinga kan representeras som produkten av magnetkonstanten m i mängden strömmar:
Integralen av B över dL = integralen av Bl över dL = m Σ In
där n är det totala antalet ledare med flerdirektionsströmmar täckta av en mentalt föreställd krets L med godtycklig form.
Varje ström beaktas i denna formel så många gånger som den täcks helt av denna krets.
Den slutliga bilden av de erhållna beräkningarna för lagen om total ström påverkas starkt av mediet i vilket den inducerade elektromagnetiska kraften (fältet) verkar.
Påverkan på miljön
De betraktade relationerna för lagen om strömmar och fält som inte fungerar i ett vakuum, utan i ett magnetiskt medium, tar en något annan form. I detta fall introduceras förutom huvudströmkomponenterna begreppet mikroskopiska strömmar som uppstår i till exempel en magnet eller i något liknande material.
Den nödvändiga relationen härleds i sin helhet från teoremet om vektorcirkulationen av magnetisk induktion B. Enkelt uttryckt uttrycks det i följande form. Det totala värdet på vektorn B när den integreras över den valda kretsen är lika med summan av makroströmmarna täckta av den multiplicerad med koefficienten för magnetkonstanten.
Som ett resultat bestäms formeln för "B" i ett ämne av uttrycket:
Integralen av B över dL = integralen av Bl över dL = m(jag+jag1)
där: dL är det diskreta elementet i kretsen riktad längs dess förbikoppling, Bl är komponenten i riktningen för tangenten vid en godtycklig punkt, bI och I1 är ledningsströmmen och den mikroskopiska (molekylära) strömmen.
Om fältet verkar i en miljö som består av godtyckliga material, bör de mikroskopiska strömmarna som är karakteristiska för dessa strukturer beaktas.
Dessa beräkningar gäller också för fältet skapat i solenoid eller i något annat medium med begränsad magnetisk permeabilitet.
Som referens
I det mest kompletta och omfattande systemet för mätning av GHS representeras magnetfältstyrkan i Oersteds (E). I ett annat befintligt system (SI) uttrycks det i ampère per meter (A / meter). Idag ersätts ostrad gradvis av en mer bekväm enhet i drift - en ampere per meter.Vid översättning av mätresultaten eller beräkningarna från SI till GHS används följande förhållande:
1 E = 1000 / (4π) A / m ≈ 79,5775 Ampere / meter.
I den sista delen av översynen noterar vi att oavsett vad ordalydelsen i lagen om fulla strömmar används förblir essensen oförändrad. Med sina egna ord kan detta representeras på följande sätt: det uttrycker förhållandet mellan strömmarna som tränger igenom en given krets och de magnetiska fälten som skapas i ämnet.
Slutligen rekommenderar vi att du tittar på en användbar video om artikelns ämne:
Relaterade material: