Hur man hittar strömstyrkan i en krets
Om kraft och spänning är kända
Anta att du behöver hitta strömstyrkan i en krets, medan du bara känner till spänningen och strömförbrukningen. För att bestämma det utan motstånd använder du formeln:
P = UI
När det är enkelt får vi en formel för beräkningar
I = P / U
Det bör noteras att detta uttryck är giltigt för DC-kretsar. Men i beräkningar, till exempel för en elmotor, beaktas dess fulla effekt eller kosinus Phi. Sedan för en trefasmotor kan det beräknas enligt följande:
Vi finner P med hänsyn till effektiviteten, vanligtvis ligger den i intervallet 0,75-0,88:
Pl = P2 / η
Här är P2 den aktiva nettoeffekten på axeln, η - effektivitet,båda dessa parametrar indikerar vanligtvis typskylten.
Vi finner den totala kraften med hänsyn till cosФ (den anges också på typskylten):
S = P1 / cosφ
Vi bestämmer den nuvarande förbrukningen med formeln:
Inom = S / (1,73 · U)
Här är 1,73 roten till 3 (används för att beräkna trefaskretsen), U är spänningen, beror på att motorn slås på (en triangel eller en stjärna) och antalet volt i nätverket (220, 380, 660, etc.). Även om i vårt land oftast finns 380V.
Om spänning eller effekt och motstånd är kända
Men det finns problem när du känner till spänningen på kretsen och lastens storlek, för att hitta strömmen utan ström, använd Ohms lag, med dess hjälp beräknar vi strömstyrkan genom motstånd och spänning.
I = U / R
Men ibland händer det att du behöver bestämma strömstyrkan utan spänning, det vill säga när du bara känner till kraften i kretsen och dess motstånd. I det här fallet:
P = UI
Dessutom, enligt Ohms samma lag:
U = IR
vad:
P = i2* R
Så vi gör beräkningen enligt formeln:
jag2= P / R
Eller ta uttrycket på höger sida av uttrycket under roten:
I = (P / R)1/2
Om EMF är internt motstånd och belastning kända
För studentproblem med en fångst finns det fall när du får EMF: s storlek och strömkällans inre motstånd. I det här fallet kan du bestämma strömstyrkan i kretsen enligt Ohms lag för en komplett krets:
I = E / (R + r)
Här är E EMF, r är strömkällans inre motstånd, och R är lasten.
Joule-Lenz lag
En annan uppgift som även en mer eller mindre erfaren student kan gå in i en stupor är att bestämma styrkan hos strömmen, om tiden, motståndet och mängden värme som frigörs av ledaren är känd.För detta minns vi Joule-Lenz lag.
Hans formel ser ut så här:
Q = I2Rt
Utför sedan beräkningen enligt följande:
jag2= QRt
Eller lägg till höger sida av ekvationen under roten:
I = (Q / Rt)1/2
Några exempel
Som en slutsats föreslår vi att fixa informationen som erhållits om flera exempel på uppgifter som du behöver för att hitta den nuvarande styrkan.
1 uppgift: Beräkna I i en krets med två motstånd för seriell anslutning och parallellanslutning. R-motstånd 1 och 2 Ohm, 12 volt strömförsörjning.
Av villkoret är det klart att du måste ge två svar för var och en av föreningarnas varianter. Sedan, för att hitta strömmen i seriekoppling, lägg först upp motståndet i kretsen för att få summan.
R1+ R2= 1 + 2 = 3 Ohm
Då kan du beräkna den nuvarande styrkan enligt Ohms lag:
I = U / R = 12/3 = 4 ampere
Med en parallell anslutning av två element kan Rtotal beräknas enligt följande:
Rtotal = (R1 * R2) / (R1 + R2) = 1 * 2/3 = 2/3 = 0,67
Sedan kan ytterligare beräkningar utföras enligt följande:
I = 12 * 0,67 = 18A
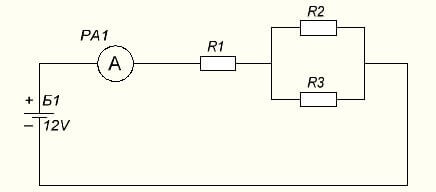
2 uppgift: beräkna strömmen för en blandad anslutning av element. Effekten från strömförsörjningen är 24V, och motstånden är: R1 = 1 Ohm, R2 = 3 Ohm, R3 = 3 Ohm.
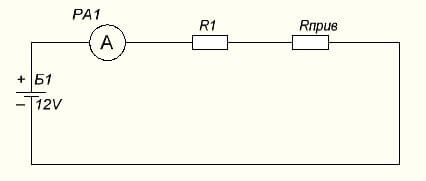
Först måste du hitta R gemensamt i parallellt anslutna R2 och R3, enligt samma formel som vi använde ovan.
Rpriv = (R2 * R3) / (R2 + R3) = (3 * 3) | (3 + 3) = 9/6 = 3/2 = 1,5 Ohm
Nu kommer kretsen att ha formen:
Därefter hittar vi strömmen enligt samma Ohms lag:
I = U / (R1 + Rpriv) = 24 / (1 + 1,5) = 24 / 2,5 = 9,6 ampere
Nu vet du hur du hittar strömstyrkan, känner till kraft, motstånd och spänning. Vi hoppas att de angivna formlerna och beräkningsexemplen hjälpte dig att lära dig materialet!
Visst vet du inte: